How to write tolerably efficient optimzation code without really trying...

...or the (freely generated module over the (min,+)-semiring)-monad. (But if I used that as a title you probably wouldn't be reading this.)

There's a large class of optimisation problems that can be considered to be about graph searching. This can include anything from finding the shortest distance between two cities, through finding the edit distance between two strings to finding the most plausible reconstruction of a signal corrupted by noise. In each case there's an obvious implementation of a solution in Haskell: use the list monad to generate all of the paths in the search space and then find the optimal path. The problem with this is that generating all paths can result in combinatorial explosion with exponential running times. So this post is about what I think is a novel monad to fix that problem. It gives a simple DSL for specifying a wide range of optimisation problems with polynomial instead of exponential complexity. In some cases it results in something close to the best published algorithm with little effort on the part of the user.

This is quite a neat and useful monad. So if the following is hard going, skip to the examples first for some motivation. I'd hate people to miss out on something that turns out to be fairly easy to use once it's set up.

Unfortunately, despite the expressiveness of Haskell making this possible, we have to fight Haskell on two fronts. One is the old annoyance of Haskell not supporting restricted monads. For a solution to that I'll refer you to Eric Kidd who used an Oleg trick. So let's get the first one out of the way before talking about graphs. Here's a preamble that replaces the Prelude's monad class with our own:

> {-# LANGUAGE MultiParamTypeClasses,
>            NoImplicitPrelude,
>            UndecidableInstances #-}

> import Debug.Trace
> import Prelude hiding ((>>=),(>>),return)
> import Data.Monoid
> import Data.Map (toList,fromListWith)

> class Monad1 m a where
>  return :: a -> m a

> class (Monad1 m a, Monad1 m b) => Monad2 m a b where
>   (>>=) :: m a -> (a -> m b) -> m b
>   (>>) :: m a -> m b -> m b
>   l >> f = l >>= \_ -> f

> class MonadPlus m where
>    mzero :: m a
>    mplus :: m a -> m a -> m a

So here's a graph with lengths marked on the edges:

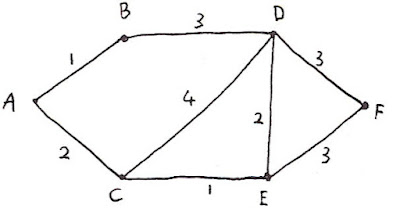
Suppose we want to find the shortest path from A to F in 3 hops. Before solving that, consider a more general problem. In the following graph

suppose we wish to find the shortest n-hop paths from A to the C_i. No matter what complexity is in the cloud, each of the paths must travel through one of the B_i. So we can solve the shortest paths problem by finding the shortest (n-1)-hop paths to the B_i and using:

dist_n(A,C_i) = min_j(dist_n-1(A,B_j)+d_ji)

Here's the crucial point to notice: If we consider dist_n(A,B_i) to be a vector whose indices are labelled by i, and d_ji to be a matrix, then the above formula is an ordinary matrix multiplication except that instead of addition and multiplication we use min and addition. If you've studied graph algorithms you'll recognise this as the same multiplication that appears in the Floyd-Warshall algorithm. If we extend the real numbers with infinity, then (R∪∞,min,+) forms a semiring. (See Cormen, Leiserson & Rivest for some good discussion of semirings in this context.) Just as you can form vector spaces over a field, you can form modules over this semiring. And just as vector spaces form a monad, so do these modules. But you don't need to know much about semirings because the monad itself is a fairly straightforward object.

Here's that infinity I was talking about:

> infinity :: Fractional a => a
> infinity = 1/0

I have to admit, I enjoyed writing that line of code :-) More importantly, Haskell does the right thing with infinities.

The monad is going to represent the length of a path to a graph vertex. Here's the definition:

> data M l p a = M { runM :: [(a,p,l)] } deriving (Eq,Show,Ord)

Ignore the l part for now, that's going to serve as a place to make a log, like the Writer monad. We'll need that when we want the actual shortest path, not just its length. For now we'll just use an empty list. So suppose that at some stage in our computation we've reached the node B with a shortest path of length 3 and node F with a shortest path of length 4. We represent this as

u = M [(B,3,[]),(F,4,[])] :: M Vertex Float [()]

.
Suppose we now consider what happens at the next step. We can express the options from B with

v = M [(A,1,[]),(D,3,[])]

and those from F as

w = M [(D,3,[]),(E,3,[])].

To combine these with the earlier computed paths we could replace B and F in u with v and w respectively to get:

M [(M [(A,1,[]),(D,3,[])],3,[]),(M [(D,3,[]),(E,3,[])],4,[])] :: M (M Vertex Float [()]) Float [()].

We need to reduce this back down to a M Vertex Float [()] using the matrix 'multiplication' formula above to pick the appropriate shortest path each time. But note the pattern: it's the usual M M a -> M a monad pattern. So we can write the substitution+reduction as an implementation of >>=. Here's the implementation, along with some other monadic goodness:

> instance (Ord a,Monoid l,Num p) => Monad1 (M l p) a where
>   return a = M [(a,0,mempty)]

> instance (Ord a,Monoid l,Fractional p,Ord b,Ord p,Ord l) => Monad2 (M l p) a b where
>   M x >>= f = let
>        applyf = [(f a,p,l) | (a,p,l) <- x]
>        rawresult = concat [[(a',(p+p',l `mappend` l')) | (a',p',l') <- a] | (M a,p,l) <- applyf]
>        reduced = map (\(a,(p,l)) -> (a,p,l)) $ toList $ fromListWith min $ rawresult
>        filtered = filter (\(_,p,l) -> p/=infinity) reduced
>        in M filtered

> instance MonadPlus (M l p) where
>    mzero = M mempty
>    mplus (M a) (M b) = M (a ++ b)

> guard True = return ()
> guard False = mzero

> choose x = M $ map (\(a,p) -> (a,p,mempty)) x

I've also had to provide my own implementation of MonadPlus. choose is a convenience function so we don't have to keep entering those empty lists.

So here's that graph represented in terms of a function that describes transitions from vertex to vertex:

> data Vertex = A | B | C | D | E | F deriving (Eq,Show,Ord)

> graph A = choose [(B,1),(C,2)]
> graph B = choose [(A,1),(D,3)]
> graph C = choose [(A,2),(D,4),(E,1)]
> graph D = choose [(B,3),(C,4),(E,2),(F,3)]
> graph E = choose [(C,1),(D,2),(F,3)]
> graph F = choose [(D,3),(E,3)]

And here's our first example. We compute all of the shortest 3-hop paths from A:

> ex0 :: M [()] Float Vertex
> ex0 = do
>    step1 <- return A
>    step2 <- graph step1
>    step3 <- graph step2
>    step4 <- graph step3
>    return step4

Just in case you think that's the wrong result note that these are the shortest paths to each accessible vertex that are exactly 3 hops long. If you want paths up to 3 hops long you have to add some zero length transitions from nodes to themselves. I'll leave that as a (trivial) exercise.

But suppose you just want the shortest path to F. Then you can use:

> ex1 :: M [()] Float Vertex
> ex1 = do
>    step1 <- return A
>    step2 <- graph step1
>    step3 <- graph step2
>    step4 <- graph step3
>    guard $ step4==F
>    return step4

Note how simple this code is. We just write code to walk the graph. All of the optimisation machinery is hidden in the background. But there's a dark secret here because the code isn't yet doing what a claim. But before I admit what the problem is, let's modify this code so we can actually see what the shortest paths are. record is just like tell from the Writer monad. I've implemented >>= so that it does the right thing:

> record l = M [((),0,l)]

> ex2 = do
>   step1 <- choose [(A,0),(B,0)]
>   record [step1]
>   step2 <- graph step1
>   record [step2]
>   step3 <- graph step2
>   record [step3]
>   step4 <- graph step3
>   record [step4]
>   guard (step4==E || step4==F)
>   return (step1,step4)

Just for fun I made this example more complex. It finds all four shortest paths from anywhere in {A,B} to anywhere in {E,F}. As an exercise try modifying the above code so that it finds the one shortest path from {A,B} to {E,F}. It's also simple to modify it to deal with conditions like the traveller being at one of a particular set of nodes at a particular time. It's a DSL, you have considerable freedom to form whatever conditions you want.

And now it's time to reveal the secret. Although I wrote >>= so that it reduces the list of considered paths at each stage the above code still has exponential complexity as you'll rapidly discover as you increase the number of steps.

Consider the third monad law: (m >>= f) >>= g = m >>= (\x -> f x >>= g).

If we evaluate the left hand side for this monad we get a reduction after applying f and then another after applying g. But we if we evaluate the right hand side we find that we get many small (and useless) reductions applied and then at the end a large reduction is applied. We don't get a big reduction at the intermediate step. The result: exponential complexity because the code ends up exploring every possible path performing stupid trivial reductions at each step. The monad law says we get the same result, but it doesn't take the same time.

And here's the really annoying thing: when you use do-notation in the usual way the Haskell compiler builds expressions like the slow right hand side. Bummer! But there's an easy, if tedious, fix. We have to use the third monad law as a rewrite rule to convert our code to the form on the left hand side. Here's ex2 rewritten:

> ex3 = do
>   step1 <- choose [(A,0),(B,0)]
>   step4 <- do
>       step3 <- do
>           step2 <- do
>               record [step1]
>               graph step1
>           record [step2]
>           graph step2
>       record [step3]
>       graph step3
>   do
>       record [step4]
>       guard (step4==E || step4==F)
>   return (step1,step4)

Not as pretty is it? It's still not too bad but it'd be nice to make this conversion automatic. I've a hunch this can be done using Haskell rules. Anyone care to volunteer some help making this work?

Anyway, I mentioned that lots of problems are in this class, some not obviously graph theoretical. Here's one: computing the edit distance between two strings:

> diag (a:as,b:bs) = choose [ ((as,bs),if a==b then 0 else 1) ]
> diag _           = mzero

> right (a:as,bs) = choose [((as,bs),1)]
> right _         = mzero

> down (as,b:bs) = choose [((as,bs),1)]
> down _         = mzero

> nop ([],[]) = return ([],[])
> nop _       = mzero

> munch :: (String,String) -> M [()] Float (String,String)
> munch x = diag x `mplus` right x `mplus` down x `mplus` nop x

> pure (M a) = length a==1
> editDistance a b = until pure (>>= munch) (munch (a,b))

> ex4 = editDistance "hypocrisy" "hippocracy"

I think this is actually the dynamic programming algorithm in disguise (and slightly reordered) with some extra log time penalties because it's using a binary tree (from Data.Set) instead of arrays. But I wouldn't stake my life on it.

Anyway, here's one last example. Rather than explain it I refer you to the nicely written Wikipedia on the Viterbi algorithm. In fact, I decided to lift their example precisely. And note that I've (1) written the code twice, the second one is the one rewritten for speed, (2) used logarithms to convert the multiplications to additions and (3) 'unrolled' the loop to make absolutely explicit what's going on. If I wrote Haskell code to work on general arrays like the Python code in the Wikipedia article, it'd be too short and you might miss it if you blinked.

> data Weather = Rainy | Sunny deriving (Eq,Show,Ord)
> data Activity = Walk | Shop | Clean deriving (Eq,Show,Ord)

> transition Rainy = choose [(Rainy,-log 0.7),(Sunny,-log 0.3)]
> transition Sunny = choose [(Rainy,-log 0.4),(Sunny,-log 0.6)]

> emission Rainy = choose [(Walk,-log 0.1),(Shop,-log 0.4),(Clean,-log 0.5)]
> emission Sunny = choose [(Walk,-log 0.6),(Shop,-log 0.3),(Clean,-log 0.1)]

> ex5 = do
>       day1 <- choose [(Rainy,-log 0.6),(Sunny,-log 0.4)]
>       record [day1]
>       emission1 <- emission day1
>       guard (emission1 == Walk)
>       day2 <- transition day1
>       record [day2]
>       emission2 <- emission day2
>       guard (emission2 == Shop)
>       day3 <- transition day2
>       record [day3]
>       emission3 <- emission day3
>       guard (emission3 == Clean)
>       day4 <- transition day3
>       record [day4]

> ex6 = do
>       day4 <- do
>           day3 <- do
>               day2 <- do
>                   day1 <- choose [(Rainy,-log 0.6),(Sunny,-log 0.4)]
>                   do
>                       record [day1]
>                       do
>                           emission1 <- emission day1
>                           guard (emission1 == Walk)
>                   transition day1
>               do
>                   record [day2]
>                   do
>                       emission2 <- emission day2
>                       guard (emission2 == Shop)
>               transition day2
>           do
>               record [day3]
>               do
>                   emission3 <- emission day3
>                   guard (emission3 == Clean)
>           transition day3
>       record [day4]

[Sunny,Rainy,Rainy,Rainy]. It's the Viterbi algorithm for free.

Anyway, I haven't proved a thing above. I think (hope?) I'm right about the polynomial complexity. Certainly on paper it all works, but I've always found it hard to reason about the complexity of Haskell code.

Unfortunately this code is all still slower than I'd like. I've played with trace during the development and everything seemed to run the way I expect (at least after I discovered the third monad law problem). I think that ultimately there's a big overhead for piling up HOFs, and the lookups in Data.Set probably aren't helping. Still, I don't think that invalidates the mathematics behind the approach and I think that asymptotically the slowness is really a big constant and a bunch of logs and it's still much better than combinatorial search. I ought to see how ocaml fares.

BTW There's a deep connection between this monad and the quantum mechanics one. I've no time to write about that now, though see here.

Some acknowledgements: the strange but highly readable Wikipedia article motivated me to think about the Viterbi algorithm, and I became sure there was a monad lurking in the Python code. I spent a month or so getting nowhere. And then I spoke with Eric Kidd on the phone about probability monads. He challenged me on something and in an attempt to formulate a response the whole of the above seemed to just crystallise. Thanks for asking the right question Eric!

I think there might be a comonad for working backwards through the graph...

Anyway, one last thing: please for the love of the FSM will someone put a clean way to implement restricted monads into their Haskell compiler. There is so much neat stuff that could be implemented with it and I now officially consider Haskell broken without one.