Comonadic Arrays

On haskell-cafe, ajb, aka Pseudonym, laments that many people don't have enough experience with comonads to recognise them. So I thought I'd mention a really simple example of a comonad that nevertheless captures the essence of a large class of comonads. It's conceptually not much different to my cellular automaton example (making this a bit of a rerun), but this should be easier to understand. And if it's too trivial, I hint at a particle physics connection towards the end.

Firstly, you can skip this paragraph if you don't want a quick bit of theoretical discussion. Consider arrays of fixed dimension. As types, they look something like X^N for some fixed integer N. From a container we construct its zipper by applying X d/dX. In this case we get XNX^N-1=NX^N. In other words, the corresponding zipper is an array paired with an index into the array. We can stretch the meaning of comonad slightly to allow this to relate to arrays whose size isn't fixed.

So here's some code:

> import Data.Array

The usual definition of Comonad:

> class Functor w => Comonad w where
>  (=>>) :: w a -> (w a -> b) -> w b
>  coreturn :: w a -> a

And now a type that is a pair of an array and an index into that array:

> data Pointer i e = P i (Array i e) deriving Show

Think of it as an array with one of its elements singled out for special attention. It trivially inherits the functoriality of ordinary arrays:

> instance Ix i => Functor (Pointer i) where
>   fmap f (P i a) = P i (fmap f a)

And now comes the Comonad implementation. coreturn serves to pop out the special element from its context - in other words it gives you the special element, whle throwing away the array it lived in. (=>>), on the other hand, applies a function f of type P i a -> b to the entire array. The function is applied to each element in turn, making each element the special element for long enough to apply f.

> instance Ix i => Comonad (Pointer i) where
>   coreturn (P i a) = a!i
>   P i a =>> f = P i $ listArray bds (fmap (f . flip P a) (range bds))
>       where bds = bounds a

Compare with fmap for arrays. This walks through each element in turn, applying a function to each element, and return an array of results. The computation for each element is separate from all the others. With =>> however, the entire array may be used for the computation of each element of the result, with the index into the array serving to indicate which element it is we should be focussing on.

For example, here's an array of values:

> x = listArray (0,9) [0..9]

We want to consider this to be a circular array so that going off one end wraps around to the beginning:

> wrap i = if i<0 then i+10 else if i>9 then i-10 else i

Now here's a simple operation that 'blurs' the single ith pixel in the 1-D image represented by x:

> blur (P i a) = let
>       k = wrap (i-1)
>       j = wrap (i+1)
>   in 0.25*a!k + 0.5*a!i + 0.25*a!j

We can apply this to the entire image thusly

> test1 = P 0 x =>> blur

Note the curious way I have to use P 0 x as an input to blur. There seems to be a redundancy here, we want the resulting array and don't care what the focussed element is. But =>> wants us to give it a focal point. Curiously it's making explicit something that's familiar to C programmers, but is slightly hidden in C. In C, you refer to an array of floats using a float *. But the same type points to elements of the array as well. So when you point to an array, you are, in effect, blurring the distinction between a pointer to an array and a pointer to the first element. Comonads make that distinction explicit.

Anyway, suppose you wanted to apply a sequence of operations. Adding, blurring, scaling, nonlinearly transforming and so on. You could write a pipeline like

> x ==> f = f x
> test2 = P 0 x ==> fmap (+1) =>> blur ==> fmap (*2) ==> fmap (\x -> x*x)

Note how ==> fmap f ==> fmap g = ==> fmap (g . f). If you think of fmap as farming out workloads to a SIMD processor with one thread applied to each array element, sequences of fmaps correspond to threads that can continue to work independently. The comonadic operations, however, correspond to steps
where the threads must synchronise and talk to each other. I believe this last statement explains the a cryptic comment in the comments to this blog entry.

One final thing going back to my optional paragraph above. If D means d/dX then we can see the operator XD as a kind of number operator. When you apply it to an array like X^N the array becomes multiplied by a type corresponding to the array index type. For ordinary arrays, these are just integers. So you can see XD as a way of counting how many elements there are in a container. Also, for any container F, we also have the equations D(XF) = XDF+F, which we can write as DX=XD+1. At some point, when I have time, I'll point out how this is closely related to the Heisenberg uncertainty principle and how when we say that differentiation makes holes in a data type, it's related to the notion of a hole in solid state physics.

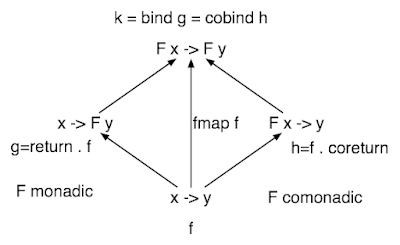
Oh, and I sketched this diagram but don't have time to write an explanation: