What can we measure? Part II

If you followed Part I then I should now be able to give an accessible lead in to some of the stuff John Baez has been talking about over the years.

So far I've illustrated examples of Hadwiger's theorem and showed how Hadwiger's 0-volume corresponds to the Euler characteristic (at least for certain finite unions of bounded shapes). Note how the r-volume has the dimensions of length^r meaning that the Euler characteristic is the only possible dimensionless quantity that is rotation- and translation-invariant and finitely additive. The Euler characteristic of a finite subset of Rⁿ is simply the cardinality of the subset. And because any kind of notion of cardinality probably ought to have the invariance properties I mention above, it looks like the Euler characteristic might provide a weird alternative to the usual notion of cardinality, despite the fact that it assigns the negative value -1 to the interval (0,1) in R. It certainly behaves a lot like cardinality and it has the additive property that you'd expect cardinality to have. It gets even better, it also have the right multiplicative property. In particular, for the kind of polyhedra objects I talked about in Part I, v₀(A×B)=v₀(A)v₀(A). But that's not all.

From now on I'll write the more usual χ instead of v₀. If you have two finite sets, A and B, then the set of functions from A to B is written B^A (at least if you're not a Haskell programmer). It's also standard stuff that for finite sets #(B^A)=#B^#A. Amazingly, if you compute the Euler characteristic in the right way, it makes sense to say that χ(B^A)=χ(B)^χ(A) for many other kinds of set too, despite the fact that χ(A) can now end up taking on negative, rational or even irrational values. χ is simply begging to be interpreted as an alternative way to count things!

If you take a peek at what Propp and Baez have to say about this you'll see that despite all of this tantalising evidence, there isn't yet a solid theory that says what any of this really means. In order to compute Euler characteristics, both Propp and Baez find themselves carrying out bizarre computations like

1+2+4+8+…=Σ_n=0…xⁿ (where x=2) =1/(1-x)=1/(1-2)=-1

(or these) which seem to give an Euler characteristic that's consistent with the other things that have been computed, and yet this computation, in itself, is nonsensical. It's clear that not only are we not sure how to answer the questions we can pose about the Euler characteristic, we're not even sure what the right questions are, or even what concepts we should be using. These are exciting times and I'm hoping that a slew of great mathematics should develop out of this over the years.

Anyway, to get back on topic. It's not just counting that's at issue, from the above summation we can see that the ordinary notion of the sum of a series is also problematic, in particular the notion of a sum of an infinite series. So let's think back to how we define such sums. We consider the sequence of partial sums and then take the limit - for every ε there is a δ such that.... In other words, to form such a limit we have to use ideas from metric spaces. So starting with an algebraic concept, the finite sum, we make the 'leap' to infinite sums by importing machinery from analysis. It's now so ingrained into us that despite the fact that ordinary summation is an algebraic concept, we understand the sum to mean a concept from analysis. But as Hadwiger's theorem shows, there are ways of making the leap to sums over infinite sets without using analysis. Conventionally we count the size of a structure by throwing away most of the structure so we're left with nothing but some underlying set, and then we use the fact that we already have a theory of cardinality for these bare sets. But what Baez & co. have been pointing out is that there seem to be alternative notion of cardinality that compute the size of something directly without throwing away the structure. We can go straight from object→number rather than going object→set→number. (Baez would say something about how we're working in a category other than Set.)

So why does this matter? Have a look at the beginning of these notes by Richard Borcherds. (Aside: I'm completely out of academic social circles these days so it's an utterly amazing coincidence that I bumped into him at a party a few weeks ago and he told me he was into QFT these days.) From the beginning it's dealing with the question of how to compute integrals that diverge. In QFT we compute the probability of something happening by summing over all of the possible ways it could happen. But this space of all possible ways is incredibly large - infinite dimensional in fact. Analysis fails us - as Borcherds points out on page 2, there is no Lebesgue measure on this space meaning we can't hope to perform this summation in the conventional way. Physicists end up having to perform nonsensical calculations just like the one above to get their answers. It seems like physicists are also using the wrong kind of summation. Maybe the Euler characteristic isn't just abstract nonsense but is actually the tool we ned in physics.

So here's my take on all this: the reason we use the sum to refer to a concept from analysis is that analysts were the first people to give a rigorous definition of an infinite sum. Maybe if a combinatorialist like Propp had got there first we'd be using a different notion. In particular, physicists all try to compute their sums in an analytic way and get into a mess as a result. The whole field of renormalisation is one horrific kludge to work around the fact that infinities crop up all the way through the work of physicists. Maybe we need to find a new way to count that doesn't throw away our underlying structures and so can give us sensible answers.

For example, consider bosonic string theory. (And by doing this I'm not in any way trying to endorse String Theory. I just happen to know some of the mathematics behind it. Physicists are very polarised over whether or not it's a good physical model, and just mentioning the field is enough for them to think you have joined one camp or another. It's just a good 'toy' model.) To get sensible answers we have to go through the usual shenanigans to get finite numbers. But there's a really neat parallel with Hadwiger's theorem. Just as insisting on rotation- and translation-invariance narrows down the possible notions of cardinality, in String Theory conformal-invariance pins down the possible ways we might sum over all paths. In fact, it pins things down so well that not only is there only one possible way to carry out our summation, it shows that this summation only makes sense in 26 dimensions. So what is this space we're summing over? Well as a string moves through space it sweeps out a surface called a worldsheet:

So we're looking at summing over the space of all possible 2D surfaces of a certain type. These are known as moduli spaces. In particular, if we want to sum over all of these surfaces, we must start by summing over all such surfaces with one loop in them, ie. sum over all toruses. We need to consider the space of all such toruses. Turns out there's a nice way of looking at this space. I won't spell out the details but the space looks like the shaded region below

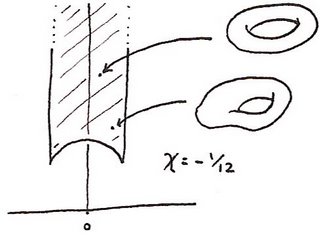
folded up in a certain way. (The 'certain way' is described here.) The folded up space is an example of an orbifold. Each point in this space corresponds to one torus so every possible path that a string can take that sweeps out a surface with one 'hole' corresponds to one point in this space. And John Conway et al. have written a nice document on how to compute the Euler number of an orbifold and this one has an Euler characteristic of -1/12.

I'll come back to this in a moment. But there's another approach to String Theory. Again, I'm not going to any kind of detail. But part of the calculations require looking at the vibration modes of a string. Just like with a musical instrument you get a fundamental 'note' and higher overtones. When a quantum string string is in its lowest energy state it has some of its energy stored in each mode of vibration. If the lowest mode of vibration has 1 unit of energy, the first overtone has 2, the second has 3 and so on. So when we try to find the total energy of a string in its lowest energy state, part of the computation requires summing 1+2+3+4+…. It's one of these apparently meaningless sums but physicists can use a trick called zeta regularisation to get the result -1/12. It's the same number as above but arrived at in a completely different way.

So here's my theory about what's going on. (Unlike other people out there who are crackpots, I have the decency to warn you when I might be grossly misunderstanding other people or even making stuff up. :-) The problem is that physicists keep getting infinities because they have to compute these infinite sums. And they start to calculate these sums by 'creeping up on them', ie. by taking the limit as you compute each of the partial sums. They're trying to use the analyst's definition of summation using deltas and epsilons. Unfortunately, the things physicists are trying to sum over are so large there simply isn't a way to creep up on infinity like this. So instead, I think we have to redefine what we mean by counting and summation. Instead we should be using the Euler characteristic. The -1/12 above is a clue that this is the right track - because when physicists try to use their weird renormalisation tricks to get answers it's not unusual for the result to end up having a mysterious Euler number connection. So it's as if the weird tricks are just a shadow of some deeper kind of mathematics that one day will make sense. But we can't just sum over any old set in this way - there needs to be some other structure that tells us how to compute these sums. In the case of Hadwiger's theorem, if we assume the sums are dimensionless and invariant under rotations and translations then that is enough information to pin down precisely one possible meaning of the sum - the Euler characteristic. What John Baez and co. are doing is trying to find other kinds of structures that are relevant for physical theories and I'm hoping that one day these will lead to a new notions of summation that work for them.

I've drifted a bit from my original topic - a chapter in a course from a graphics convention, so I'll stop there. But here's the one paragraph summary of what I'm saying: just as we can count the elements in a set, there is also a notion of counting for other kinds of structure. We don't really have a proper theory of what this means but we do have some partial results that suggest the Euler characteristic is connected somehow. And maybe when we have a proper theory, and literally a new way to count, the problems with infinities that plague any kind of quantum field theory will go away.