Arboreal Isomorphisms from Nuclear Pennies
The game of Nuclear Pennies is a game for one player played on a semi-infinite strip of sites, each of which may contain any non-negative number of pennies. The aim is to achieve a target configuration of pennies from a starting configuration by means of penny fusion and penny fission. In penny fission, a penny is split into a pair of pennies in the two neighbouring sites. In penny fusion, two pennies, separated by exactly one site, are fused into one penny in the intervening site. Obviously no fission or fusion take place at the very end site because there is no room for one of the fission products or fusion precursors. The following diagrams show some legal moves in Nuclear Pennies:
One using fission:

One using fusion:

Can you achieve this target configuration:

Starting from this configuration?

It's a surprisingly non-trivial task but I urge you to have a go. If you give up, here's a video solution:
So a natural question arises: what single penny configurations can be achieved from that starting position? As every move in Nuclear Pennies is reversible, if you solved the puzzle you know we can shift a single penny 6 places left or right. (But to move 6 spaces left we need one extra space on the left.) So labelling positions 0,1,2,... we know that starting from 7 we can place a penny on 6n+1 for all non-negative n. But what about other positions?
We can borrow a technique from M Reiss's seminal paper on peg solitaire: Beiträge zur Theorie des Solitär-Spiels, Crelles Journal 54 (1857) 344-379. The idea is to associate an algebraic value with each position and then ensure that each this is chosen so that each legal move leaves the value unchanged.
Label the sites as follows:

We consider the value of each penny to be the value of its site and to get the value of a position, add the values of the individual pennies. If we pick x to be one of the complex cube roots of -1 then we have x=x2+1, because x3+1=(1+x)(x2+1-x). We define a move to be paralegal if it doesn't change the value of a position. It should be clear that penny fusion and fission are both paralegal. In other words
and
Now consider the values of 1,x,x2,... and so on. It's not hard to show that the only time an element in this sequence takes the value 1 is when the exponent is 6. In fact, x is a sixth root of unity. So this shows we can never shift a single coin by anything other than a multiple of 6 sites. As the video shows how to shift by 6 sites we know we can shift a single coin by n sites if and only if n is a multiple of 6 (and there's one site available to the left of the leftmost penny). It's neat that we took an excursion through the field of complex numbers to prove something about a seemingly simple piece of discrete mathematics.
But who cares about nuclear coin reactions? That's not my real motivation here. Believe it or not, each coin shuffle above corresponds to an isomorphism between certain types and solving the puzzle above actually demonstrates a really neat isomorphism between tuples of data structures.
Go back to the algebra above. We have that legal ⇒ paralegal because coin reactions correspond to legal manipulations of x. Fissioning a coin represents replacing x by 1+x2, for example. But the converse isn't true. We can manipulate complex numbers in all kinds of interesting ways that don't correspond to coin reactions. For example, we can write -x2 but we aren't allowed negative numbers of coins in a site. But there's another algebraic structure which corresponds exactly to coin reactions. To see that, it's time to start writing Haskell code:
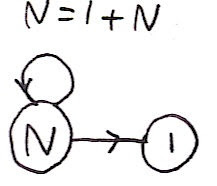
T is a simple binary tree type. That declaration simply says that in the algebra of types, T=T2+1. Now unlike complex numbers, when you form a polynomial in the type T you can't have anything other than a non-negative integer as a coefficient. In other words, positions in the game of Nuclear Pennies correspond precisely to polynomials, in the algebra of types, in T.
For example, consider the first move in the video solution I gave:

It corresponds to
or in Haskell notation an isomorphism
So you know what I'm going to do next, I'm going to code up the entire solution as a Haskell program mapping seven trees to one and back again. You don't need to read all of the following, but I thought I'd put it here for completeness. So skip over the code to the end if you feel like it...
Firstly, Either is a bit tedious to write. So here's my own implementation that uses a slightly non-standard way to write a type constructor:
We know that the type algebra is commutative, so A+B=B+A. But that '=' sign is really an isomorphism, not equality, and we'll need that isomorphism explicitly:
Same goes for associativity:
And associativity the other way. Here I'm starting a convention of using primes to represent the inverse of a function.
For a fixed b, '+b' is a functor so f :: a -> b induces a map a+b -> c+b. Unfortunately I don't know an easy way to make '+b', as opposed to 'b+', a functor in Haskell. So I'll have to make do with this function that lifts f to a+b:
I'm going to need all these.
I'm going to represent tuples a little weirdly, though arguably this is much more natural than the usual way to write tuples. Tn corresponds to Tn:
And now we need functions to assemble and disassemble trees at the start of a tuple. These correspond to fusion and fission respectively in the game.
Here's the first step in the solution. That was easy.
It gets successively harder because we need to push the assemble' function down into the type additions:
We're going to use a few functions whose sole purposes is to shuffle around type additions using commutativity and associativity.
After the left-to-right sweep, here's the right-to-left sweep:
And now we have another left-to-right sweep followed by a right-to-left sweep:
And put it all together:
At this point I might as well write the inverse. This was mostly derived from the forward function using vim macros:
Enough already! Time to test the code. It's already pretty obvious that each of the steps above is invertible but let's use QuickCheck anyway. And here's a small puzzle: why to I have return Leaf twice?
All done.
So time to think about what exactly we have here. We have a way to pack 7-tuples of trees into a single tree exactly. It's easy to store two trees in a tree say, just by making them the left and right branch of another tree. But then we get some 'wastage' because the isolated leaf doesn't correspond to any pair of trees. We have a perfect packing. Of course the set of trees and the set of 7-tuples of trees have the same cardinality, and it's not hard to find a bijection by enumerating these sets and laying them out side by side. But such a bijection could get arbitrarily complicated. But the isomorphism above only looks at the tops of the trees and can be executed lazily. It's a particularly nice isomorphism. And from what I showed above, you can only pack (6n+1)-tuples into a single tree. Weird eh?
And everything I say here is derived from the amazing paper Seven Trees in One by Andreas Blass. I've mentioned it a few times before but I've been meaning to implement the isomorphism explicitly for ages. Blass's paper also shows that you can, to some extent, argue paralegal ⇒ legal - something that's far from obvious.
One using fission:

One using fusion:

Can you achieve this target configuration:

Starting from this configuration?

It's a surprisingly non-trivial task but I urge you to have a go. If you give up, here's a video solution:
So a natural question arises: what single penny configurations can be achieved from that starting position? As every move in Nuclear Pennies is reversible, if you solved the puzzle you know we can shift a single penny 6 places left or right. (But to move 6 spaces left we need one extra space on the left.) So labelling positions 0,1,2,... we know that starting from 7 we can place a penny on 6n+1 for all non-negative n. But what about other positions?
We can borrow a technique from M Reiss's seminal paper on peg solitaire: Beiträge zur Theorie des Solitär-Spiels, Crelles Journal 54 (1857) 344-379. The idea is to associate an algebraic value with each position and then ensure that each this is chosen so that each legal move leaves the value unchanged.
Label the sites as follows:

We consider the value of each penny to be the value of its site and to get the value of a position, add the values of the individual pennies. If we pick x to be one of the complex cube roots of -1 then we have x=x2+1, because x3+1=(1+x)(x2+1-x). We define a move to be paralegal if it doesn't change the value of a position. It should be clear that penny fusion and fission are both paralegal. In other words
legal ⇒ paralegal
and
paraillegal ⇒ illegal
Now consider the values of 1,x,x2,... and so on. It's not hard to show that the only time an element in this sequence takes the value 1 is when the exponent is 6. In fact, x is a sixth root of unity. So this shows we can never shift a single coin by anything other than a multiple of 6 sites. As the video shows how to shift by 6 sites we know we can shift a single coin by n sites if and only if n is a multiple of 6 (and there's one site available to the left of the leftmost penny). It's neat that we took an excursion through the field of complex numbers to prove something about a seemingly simple piece of discrete mathematics.
But who cares about nuclear coin reactions? That's not my real motivation here. Believe it or not, each coin shuffle above corresponds to an isomorphism between certain types and solving the puzzle above actually demonstrates a really neat isomorphism between tuples of data structures.
Go back to the algebra above. We have that legal ⇒ paralegal because coin reactions correspond to legal manipulations of x. Fissioning a coin represents replacing x by 1+x2, for example. But the converse isn't true. We can manipulate complex numbers in all kinds of interesting ways that don't correspond to coin reactions. For example, we can write -x2 but we aren't allowed negative numbers of coins in a site. But there's another algebraic structure which corresponds exactly to coin reactions. To see that, it's time to start writing Haskell code:
> import Prelude hiding (Left,Right)
> import Control.Monad
> import Test.QuickCheck
> data T = Leaf | Fork T T deriving (Eq,Show)
T is a simple binary tree type. That declaration simply says that in the algebra of types, T=T2+1. Now unlike complex numbers, when you form a polynomial in the type T you can't have anything other than a non-negative integer as a coefficient. In other words, positions in the game of Nuclear Pennies correspond precisely to polynomials, in the algebra of types, in T.
For example, consider the first move in the video solution I gave:

It corresponds to
T7->T8+T6
or in Haskell notation an isomorphism
(T,T,T,T,T,T,T) -> Either (T,T,T,T,T,T,T,T) (T,T,T,T,T,T)
So you know what I'm going to do next, I'm going to code up the entire solution as a Haskell program mapping seven trees to one and back again. You don't need to read all of the following, but I thought I'd put it here for completeness. So skip over the code to the end if you feel like it...
Firstly, Either is a bit tedious to write. So here's my own implementation that uses a slightly non-standard way to write a type constructor:
> data a :+ b = Left a | Right b
We know that the type algebra is commutative, so A+B=B+A. But that '=' sign is really an isomorphism, not equality, and we'll need that isomorphism explicitly:
> commute :: a :+ b -> b :+ a
> commute (Left a) = Right a
> commute (Right b) = Left b
Same goes for associativity:
> associate :: (a :+ b) :+ c -> a :+ (b :+ c)
> associate (Left (Left a)) = Left a
> associate (Left (Right b)) = Right (Left b)
> associate (Right c) = Right (Right c)
And associativity the other way. Here I'm starting a convention of using primes to represent the inverse of a function.
> associate' :: a :+ (b :+ c) -> (a :+ b) :+ c
> associate' (Left a) = Left (Left a)
> associate' (Right (Left b)) = Left (Right b)
> associate' (Right (Right c)) = Right c
For a fixed b, '+b' is a functor so f :: a -> b induces a map a+b -> c+b. Unfortunately I don't know an easy way to make '+b', as opposed to 'b+', a functor in Haskell. So I'll have to make do with this function that lifts f to a+b:
> liftLeft :: (a -> c) -> a :+ b -> c :+ b
> liftLeft f (Left a) = Left (f a)
> liftLeft f (Right b) = Right b
I'm going to need all these.
> liftLeft2 = liftLeft . liftLeft
> liftLeft3 = liftLeft . liftLeft2
> liftLeft4 = liftLeft . liftLeft3
> liftLeft5 = liftLeft . liftLeft4
I'm going to represent tuples a little weirdly, though arguably this is much more natural than the usual way to write tuples. Tn corresponds to Tn:
> type T0 = ()
> type T1 = (T,T0)
> type T2 = (T,T1)
> type T3 = (T,T2)
> type T4 = (T,T3)
> type T5 = (T,T4)
> type T6 = (T,T5)
> type T7 = (T,T6)
> type T8 = (T,T7)
And now we need functions to assemble and disassemble trees at the start of a tuple. These correspond to fusion and fission respectively in the game.
> assemble (Left x) = (Leaf,x)
> assemble (Right (a,(b,x))) = (Fork a b,x)
> assemble' (Leaf,x) = Left x
> assemble' (Fork a b,x) = Right (a,(b,x))
Here's the first step in the solution. That was easy.
> step1 :: T7 -> T6 :+ T8
> step1 = assemble'
It gets successively harder because we need to push the assemble' function down into the type additions:
> step2 :: T6 :+ T8 -> T5 :+ T7 :+ T8
> step2 = liftLeft assemble'
> step3 :: T5 :+ T7 :+ T8 -> T4 :+ T6 :+ T7 :+ T8
> step3 = liftLeft2 assemble'
> step4 :: T4 :+ T6 :+ T7 :+ T8 -> T3 :+ T5 :+ T6 :+ T7 :+ T8
> step4 = liftLeft3 assemble'
> step5 :: T3 :+ T5 :+ T6 :+ T7 :+ T8 -> T2 :+ T4 :+ T5 :+ T6 :+ T7 :+ T8
> step5 = liftLeft4 assemble'
> step6 :: T2 :+ T4 :+ T5 :+ T6 :+ T7 :+ T8 -> T1 :+ T3 :+ T4 :+ T5 :+ T6 :+ T7 :+ T8
> step6 = liftLeft5 assemble'
We're going to use a few functions whose sole purposes is to shuffle around type additions using commutativity and associativity.
> swap23 :: (a :+ b) :+ c -> (a :+ c) :+ b
> swap23 = commute . associate . liftLeft commute
> shuffle1 :: T1 :+ T3 :+ T4 :+ T5 :+ T6 :+ T7 :+ T8 -> T1 :+ T4 :+ T3 :+ T5 :+ T6 :+ T7 :+ T8
> shuffle1 = liftLeft4 swap23
> shuffle2 :: (T1 :+ T4) :+ T3 :+ T5 :+ T6 :+ T7 :+ T8 -> T3 :+ T5 :+ T6 :+ T7 :+ T8 :+ (T1 :+ T4)
> shuffle2 = swap23 . liftLeft swap23 . liftLeft2 swap23 . liftLeft3 swap23 . liftLeft4 commute
After the left-to-right sweep, here's the right-to-left sweep:
> step7 :: T3 :+ T5 :+ T6 :+ T7 :+ T8 :+ (T1 :+ T4) -> T4 :+ T6 :+ T7 :+ T8 :+ (T1 :+ T4)
> step7 = liftLeft4 assemble
> step8 :: T4 :+ T6 :+ T7 :+ T8 :+ (T1 :+ T4) -> T5 :+ T7 :+ T8 :+ (T1 :+ T4)
> step8 = liftLeft3 assemble
> step9 :: T5 :+ T7 :+ T8 :+ (T1 :+ T4) -> T6 :+ T8 :+ (T1 :+ T4)
> step9 = liftLeft2 assemble
> step10 :: T6 :+ T8 :+ (T1 :+ T4) -> T7 :+ (T1 :+ T4)
> step10 = liftLeft assemble
> shuffle3 :: T7 :+ (T1 :+ T4) -> T1 :+ T4 :+ T7
> shuffle3 = commute
And now we have another left-to-right sweep followed by a right-to-left sweep:
> step11 :: T1 :+ T4 :+ T7 -> T2 :+ T0 :+ T4 :+ T7
> step11 = liftLeft2 (commute . assemble')
> step12 :: T2 :+ T0 :+ T4 :+ T7 -> T3 :+ T1 :+ T0 :+ T4 :+ T7
> step12 = liftLeft3 (commute . assemble')
> step13 :: T3 :+ T1 :+ T0 :+ T4 :+ T7 -> T4 :+ T2 :+ T1 :+ T0 :+ T4 :+ T7
> step13 = liftLeft4 (commute . assemble')
> step14 :: T4 :+ T2 :+ T1 :+ T0 :+ T4 :+ T7-> T5 :+ T3 :+ T2 :+ T1 :+ T0 :+ T4 :+ T7
> step14 = liftLeft5 (commute . assemble')
> shuffle4 :: T5 :+ T3 :+ T2 :+ T1 :+ T0 :+ T4 :+ T7 -> T7 :+ T5 :+ T3 :+ T2 :+ T1 :+ T0 :+ T4
> shuffle4 = liftLeft5 commute . liftLeft4 swap23 . liftLeft3 swap23 . liftLeft2 swap23 . liftLeft swap23 . swap23
> shuffle5 :: T7 :+ T5 :+ T3 :+ T2 :+ T1 :+ T0 :+ T4 -> T7 :+ T5 :+ T4 :+ T3 :+ T2 :+ T1 :+ T0
> shuffle5 = liftLeft3 swap23 . liftLeft2 swap23 . liftLeft swap23 . swap23
> step15 :: T7 :+ T5 :+ T4 :+ T3 :+ T2 :+ T1 :+ T0 -> T6 :+ T4 :+ T3 :+ T2 :+ T1 :+ T0
> step15 = liftLeft5 (assemble . commute)
> step16 :: T6 :+ T4 :+ T3 :+ T2 :+ T1 :+ T0 -> T5 :+ T3 :+ T2 :+ T1 :+ T0
> step16 = liftLeft4 (assemble . commute)
> step17 :: T5 :+ T3 :+ T2 :+ T1 :+ T0 -> T4 :+ T2 :+ T1 :+ T0
> step17 = liftLeft3 (assemble . commute)
> step18 :: T4 :+ T2 :+ T1 :+ T0 -> T3 :+ T1 :+ T0
> step18 = liftLeft2 (assemble . commute)
> step19 :: T3 :+ T1 :+ T0 -> T2 :+ T0
> step19 = liftLeft (assemble . commute)
> step20 :: T2 :+ T0 -> T1
> step20 = assemble . commute
And put it all together:
> iso :: T7 -> T1
> iso = step20 . step19 . step18 . step17 . step16 . step15 . shuffle5 . shuffle4 . step14 .
> step13 . step12 . step11 . shuffle3 . step10 . step9 . step8 . step7 .
> shuffle2 . shuffle1 . step6 . step5 . step4 . step3 . step2 . step1
At this point I might as well write the inverse. This was mostly derived from the forward function using vim macros:
> step20' :: T1 -> T2 :+ T0
> step20' = commute . assemble'
> step19' :: T2 :+ T0 -> T3 :+ T1 :+ T0
> step19' = liftLeft (commute . assemble')
> step18' :: T3 :+ T1 :+ T0 -> T4 :+ T2 :+ T1 :+ T0
> step18' = liftLeft2 (commute . assemble')
> step17' :: T4 :+ T2 :+ T1 :+ T0 -> T5 :+ T3 :+ T2 :+ T1 :+ T0
> step17' = liftLeft3 (commute . assemble')
> step16' :: T5 :+ T3 :+ T2 :+ T1 :+ T0 -> T6 :+ T4 :+ T3 :+ T2 :+ T1 :+ T0
> step16' = liftLeft4 (commute . assemble')
> step15' :: T6 :+ T4 :+ T3 :+ T2 :+ T1 :+ T0 -> T7 :+ T5 :+ T4 :+ T3 :+ T2 :+ T1 :+ T0
> step15' = liftLeft5 (commute . assemble')
> shuffle5' :: T7 :+ T5 :+ T4 :+ T3 :+ T2 :+ T1 :+ T0 -> T7 :+ T5 :+ T3 :+ T2 :+ T1 :+ T0 :+ T4
> shuffle5' = swap23 . liftLeft swap23 . liftLeft2 swap23 . liftLeft3 swap23
> shuffle4' :: T7 :+ T5 :+ T3 :+ T2 :+ T1 :+ T0 :+ T4 -> T5 :+ T3 :+ T2 :+ T1 :+ T0 :+ T4 :+ T7
> shuffle4' = swap23 . liftLeft swap23 . liftLeft2 swap23 . liftLeft3 swap23 . liftLeft4 swap23 . liftLeft5 commute
> step14' :: T5 :+ T3 :+ T2 :+ T1 :+ T0 :+ T4 :+ T7 -> T4 :+ T2 :+ T1 :+ T0 :+ T4 :+ T7
> step14' = liftLeft5 (assemble . commute)
> step13' :: T4 :+ T2 :+ T1 :+ T0 :+ T4 :+ T7 -> T3 :+ T1 :+ T0 :+ T4 :+ T7
> step13' = liftLeft4 (assemble .commute)
> step12' :: T3 :+ T1 :+ T0 :+ T4 :+ T7 -> T2 :+ T0 :+ T4 :+ T7
> step12' = liftLeft3 (assemble . commute)
> step11' :: T2 :+ T0 :+ T4 :+ T7 -> T1 :+ T4 :+ T7
> step11' = liftLeft2 (assemble . commute)
> shuffle3' :: T1 :+ T4 :+ T7 -> T7 :+ (T1 :+ T4)
> shuffle3' = commute
> step10' :: T7 :+ (T1 :+ T4) -> T6 :+ T8 :+ (T1 :+ T4)
> step10' = liftLeft assemble'
> step9' :: T6 :+ T8 :+ (T1 :+ T4) -> T5 :+ T7 :+ T8 :+ (T1 :+ T4)
> step9' = liftLeft2 assemble'
> step8' :: T5 :+ T7 :+ T8 :+ (T1 :+ T4) -> T4 :+ T6 :+ T7 :+ T8 :+ (T1 :+ T4)
> step8' = liftLeft3 assemble'
> step7' :: T4 :+ T6 :+ T7 :+ T8 :+ (T1 :+ T4) -> T3 :+ T5 :+ T6 :+ T7 :+ T8 :+ (T1 :+ T4)
> step7' = liftLeft4 assemble'
> shuffle2' :: T3 :+ T5 :+ T6 :+ T7 :+ T8 :+ (T1 :+ T4) -> (T1 :+ T4) :+ T3 :+ T5 :+ T6 :+ T7 :+ T8
> shuffle2' = liftLeft4 commute . liftLeft3 swap23 . liftLeft2 swap23 . liftLeft swap23 . swap23
> shuffle1' :: T1 :+ T4 :+ T3 :+ T5 :+ T6 :+ T7 :+ T8 -> T1 :+ T3 :+ T4 :+ T5 :+ T6 :+ T7 :+ T8
> shuffle1' = liftLeft4 swap23
> step6' :: T1 :+ T3 :+ T4 :+ T5 :+ T6 :+ T7 :+ T8 -> T2 :+ T4 :+ T5 :+ T6 :+ T7 :+ T8
> step6' = liftLeft5 assemble
> step5' :: T2 :+ T4 :+ T5 :+ T6 :+ T7 :+ T8 -> T3 :+ T5 :+ T6 :+ T7 :+ T8
> step5' = liftLeft4 assemble
> step4' :: T3 :+ T5 :+ T6 :+ T7 :+ T8 -> T4 :+ T6 :+ T7 :+ T8
> step4' = liftLeft3 assemble
> step3' :: T4 :+ T6 :+ T7 :+ T8 -> T5 :+ T7 :+ T8
> step3' = liftLeft2 assemble
> step2' :: T5 :+ T7 :+ T8 -> T6 :+ T8
> step2' = liftLeft assemble
> step1' :: T6 :+ T8 -> T7
> step1' = assemble
> iso' :: T1 -> T7
> iso' = step1' . step2' . step3' . step4' .
> step5' . step6' . shuffle1' . shuffle2' . step7' .
> step8' . step9' . step10' . shuffle3' . step11' .
> step12' . step13' . step14' . shuffle4' . shuffle5' .
> step15' . step16' . step17' . step18' . step19' . step20'
Enough already! Time to test the code. It's already pretty obvious that each of the steps above is invertible but let's use QuickCheck anyway. And here's a small puzzle: why to I have return Leaf twice?
> instance Arbitrary T where
> arbitrary = oneof [return Leaf,return Leaf,liftM2 Fork arbitrary arbitrary]
> main = do
> quickCheck $ \x -> x==iso (iso' x)
> quickCheck $ \x -> x==iso' (iso x)
All done.
So time to think about what exactly we have here. We have a way to pack 7-tuples of trees into a single tree exactly. It's easy to store two trees in a tree say, just by making them the left and right branch of another tree. But then we get some 'wastage' because the isolated leaf doesn't correspond to any pair of trees. We have a perfect packing. Of course the set of trees and the set of 7-tuples of trees have the same cardinality, and it's not hard to find a bijection by enumerating these sets and laying them out side by side. But such a bijection could get arbitrarily complicated. But the isomorphism above only looks at the tops of the trees and can be executed lazily. It's a particularly nice isomorphism. And from what I showed above, you can only pack (6n+1)-tuples into a single tree. Weird eh?
And everything I say here is derived from the amazing paper Seven Trees in One by Andreas Blass. I've mentioned it a few times before but I've been meaning to implement the isomorphism explicitly for ages. Blass's paper also shows that you can, to some extent, argue paralegal ⇒ legal - something that's far from obvious.