Untangling with Continued Fractions: Part 3
It's time to return to the vector space monad. But first, after some Haskell preamble, I need to talk about the Einstein summation convention.
We're going to be dealing with multidimensional arrays of values that I'll call tensors. We can refer to the individual elements of these arrays by providing tuples of indices drawn from some set of indices. For example we might refer to the elements of a 10 by 10 array by using pairs of indices, each drawn from the set {0,1,2,...,9}. We'll write some indices as subscripts and some as superscripts. Here are some examples: vi, wj,Tij,Wijkl. vi means the ith value in array v, Tij means the (i,j)-th element of T and so on.
We can form sums over such indices like this
where the sum is over the corresponding index sets for j and k.
The Einstein summation convention is simply this: if an expression has an index repeated once as a subscript and once as a superscript then we implicitly assume a sum over the index without writing the summation symbol. So the above expression becomes simply
The vector space monad allows us to express something similar using do-notation. Let's use the type Bool for our index set, so we're selecting elements of our arrays using the values {False,True} rather than integers. Let ei be the (2-dimensional) vector with the property that its j-component is 1 for j=i and 0 for j≠i. In do-notation this is represented by return i. We use superscripts to indicate the components of a vector so the components of ei are eji. We can write the vector v=3eFalse-5eTruea, with components (3,-5) as
Dual to vectors we have covectors. You can think of these as linear functions that consume vectors and return reals. We can define a basis of covectors fi with the property that fi(ej) is 1 for i=j and 0 otherwise. In our Haskell code it'll be more convenient to think of covectors as mapping vectors to the one-dimensional vector space whose basis element is labelled by (). When we make a vector using an expression like return True, that True is a constructor for the type Bool. We expect to use the dual operation for covectors, and that dual is case analysis. So, for example, we can write w = fFalse+2*fTrue, wih components (1,2), as
Applying w to v gives the expression viwi using the summation convention. Using do-notation it looks like
The point to note is that just like with the summation convention, we don't need to explicitly sum over i. i serves as a kind of iterator object and a vector v automatically supplies i with values in the appropriate range. w then consumes i. So we can translate the summation convention to do-notation by thinking of upper indices corresponding to places that iterators can emerge from, and thinking of lower indices as places where iterators can be consumed.
Another example is matrix representing a transformation of a vector to a vector. It must consume one iterator and emit another one. In the Einstein summation convention such a transformation might be written ri=Mijvj. We could write a simple 2D 2x scale and 90 degree rotation matrix as
We can then write the transformation as
Another simple example is an inner product. We can represent the ordinary dot product as a matrix dij and write the square length of v as v . v = dijvivj. We can implement this as
where we define
Similarly, tuples of superscripts correspond to iterators that are tuples of indices.
With that in place, we're now in a position to consider what monadic notation for knots means in the vector-space-over Bool monad. Essentially what we're doing is representing 'components' of a tangle or knot, the cups, caps and crossings, as tensors. When we glue these components with labels we're forming sums. In fact, each labelled edge connecting two components corresponds to an index and so we can think of it as possibly taking two different values, False or True. So the monadic expression corresponds to a sum over all possible ways to assign values from Bool to the indices with a corresponding weight for each term. This should be familiar to some people, it's just like what takes place in statistical thermodynamics. We consider a bunch of particles and form a sum over all of the possible states that those particles could have, with a corresponding weight for each configuration of states. A good example is the Ising model in which electrons sit at the vertices of a regular lattice. Two neighbouring electrons in a ferromagnet tend to want to align the same way, so confgurations in which neighbouring electrons have the same spin will get assigned a higher weight.
In our tangle problem, the trick is to find a magic set of weights with the property that two different summations representing isotopic knots or tangles give the same result. This turns out to be too hard, but we relax it a bit we will be led to one of the most fruitful new approaches in knot theory in recent years - the Jones Polynomial. Vaughan Jones was investigating certain types of model from statistical mechanics and came to realise that some of the equations that were arising were the same ones needed to get suitable weights for knot theory. From this realisation emerged his eponymous polynomial. But, that's all I'll be saying about this polynomial in this post.
Anyway, to make things clearer here's an example:
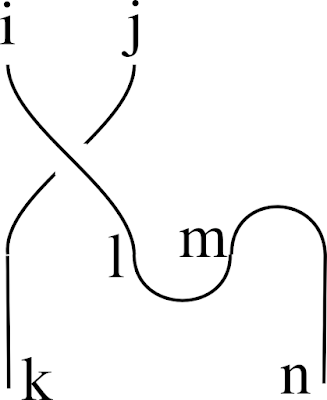
We interpret cap, cup, over and under as the tensors Mij, Nij, Sijkl and Tijkl. In monadic notation we get
With the summation convention in mind this evaluates to:
and without it we see that all we're doing is computing
We can try an elementary choice for our tensors above. We can define M and N to be given by identity matrices:
We can then choose S and T to simply swap their arguments:
With these choices, the weighting is such that a non-zero weight is assigned to a knot or tangle if and only if all of the labels along a single strand are assigned the same value, in other words we're now summing over ways of assigning labels to entire strands. For rational tangles we can only end up with three possible values corresponding to the three ways the two outputs can be connected to the two inputs. (Straight through, the tangle I called ∞; straight through with a swap, the tangle called -1; and connecting together both the inputs, and both the outputs, the tangle called 0.)
Only test2 succeeds so we know example is a tangle that forms its outputs by swapping the inputs.
So even with this simple assignment we're able to extract some basic connectivity information from our monadic representation. With smarter choices we'll get more information, but that's enough for now. We now have the prerequisites and in the next installment we can start doing some proper knot theory.
> {-# LANGUAGE MultiParamTypeClasses,FlexibleInstances,FunctionalDependencies #-}
> module Main where
> import qualified Data.Map as M
> import Control.Monad
> import Test.QuickCheck
> infixl 4 .+
> infixl 4 .-
> infixl 5 .*
We're going to be dealing with multidimensional arrays of values that I'll call tensors. We can refer to the individual elements of these arrays by providing tuples of indices drawn from some set of indices. For example we might refer to the elements of a 10 by 10 array by using pairs of indices, each drawn from the set {0,1,2,...,9}. We'll write some indices as subscripts and some as superscripts. Here are some examples: vi, wj,Tij,Wijkl. vi means the ith value in array v, Tij means the (i,j)-th element of T and so on.
We can form sums over such indices like this
ΣjkTijWjkvk
where the sum is over the corresponding index sets for j and k.
The Einstein summation convention is simply this: if an expression has an index repeated once as a subscript and once as a superscript then we implicitly assume a sum over the index without writing the summation symbol. So the above expression becomes simply
TijWjkvk
The vector space monad allows us to express something similar using do-notation. Let's use the type Bool for our index set, so we're selecting elements of our arrays using the values {False,True} rather than integers. Let ei be the (2-dimensional) vector with the property that its j-component is 1 for j=i and 0 for j≠i. In do-notation this is represented by return i. We use superscripts to indicate the components of a vector so the components of ei are eji. We can write the vector v=3eFalse-5eTruea, with components (3,-5) as
> v :: V Float Bool
> v = 3 .*return False .- 5 .*return True
Dual to vectors we have covectors. You can think of these as linear functions that consume vectors and return reals. We can define a basis of covectors fi with the property that fi(ej) is 1 for i=j and 0 otherwise. In our Haskell code it'll be more convenient to think of covectors as mapping vectors to the one-dimensional vector space whose basis element is labelled by (). When we make a vector using an expression like return True, that True is a constructor for the type Bool. We expect to use the dual operation for covectors, and that dual is case analysis. So, for example, we can write w = fFalse+2*fTrue, wih components (1,2), as
> w :: Bool -> V Float ()
> w i = case i of
> False -> return ()
> True -> 2 .* return ()
Applying w to v gives the expression viwi using the summation convention. Using do-notation it looks like
> vw :: V Float ()
> vw = reduce $ do
> i <- v
> w i
The point to note is that just like with the summation convention, we don't need to explicitly sum over i. i serves as a kind of iterator object and a vector v automatically supplies i with values in the appropriate range. w then consumes i. So we can translate the summation convention to do-notation by thinking of upper indices corresponding to places that iterators can emerge from, and thinking of lower indices as places where iterators can be consumed.
Another example is matrix representing a transformation of a vector to a vector. It must consume one iterator and emit another one. In the Einstein summation convention such a transformation might be written ri=Mijvj. We could write a simple 2D 2x scale and 90 degree rotation matrix as
> m :: Bool -> V Float Bool
> m j = case j of
> False -> 2 .*return True
> True -> -2 .*return False
We can then write the transformation as
> r = do
> j <- v
> i <- m j
> return i
Another simple example is an inner product. We can represent the ordinary dot product as a matrix dij and write the square length of v as v . v = dijvivj. We can implement this as
> v2 = do
> i <- v
> j <- v
> d (i,j)
where we define
> d (i,j) = case (i,j) of
> (False,False) -> return ()
> (True,True) -> return ()
> otherwise -> mzero
Similarly, tuples of superscripts correspond to iterators that are tuples of indices.
With that in place, we're now in a position to consider what monadic notation for knots means in the vector-space-over Bool monad. Essentially what we're doing is representing 'components' of a tangle or knot, the cups, caps and crossings, as tensors. When we glue these components with labels we're forming sums. In fact, each labelled edge connecting two components corresponds to an index and so we can think of it as possibly taking two different values, False or True. So the monadic expression corresponds to a sum over all possible ways to assign values from Bool to the indices with a corresponding weight for each term. This should be familiar to some people, it's just like what takes place in statistical thermodynamics. We consider a bunch of particles and form a sum over all of the possible states that those particles could have, with a corresponding weight for each configuration of states. A good example is the Ising model in which electrons sit at the vertices of a regular lattice. Two neighbouring electrons in a ferromagnet tend to want to align the same way, so confgurations in which neighbouring electrons have the same spin will get assigned a higher weight.
In our tangle problem, the trick is to find a magic set of weights with the property that two different summations representing isotopic knots or tangles give the same result. This turns out to be too hard, but we relax it a bit we will be led to one of the most fruitful new approaches in knot theory in recent years - the Jones Polynomial. Vaughan Jones was investigating certain types of model from statistical mechanics and came to realise that some of the equations that were arising were the same ones needed to get suitable weights for knot theory. From this realisation emerged his eponymous polynomial. But, that's all I'll be saying about this polynomial in this post.
Anyway, to make things clearer here's an example:

We interpret cap, cup, over and under as the tensors Mij, Nij, Sijkl and Tijkl. In monadic notation we get
> example (i,j) = do
> (k,l) <- over (i,j)
> (m,n) <- cap
> cup (l,m)
> return (k,n)
With the summation convention in mind this evaluates to:
SijklNlmMm,n
and without it we see that all we're doing is computing
Σl,mSijklNlmMm,n
We can try an elementary choice for our tensors above. We can define M and N to be given by identity matrices:
> cap :: V Float (Bool,Bool)
> cap = return (False,False) .+ return (True,True)
> cup :: (Bool,Bool) -> V Float ()
> cup (i,j) = case (i,j) of
> (False,False) -> return ()
> (True,True) -> return ()
> otherwise -> mzero
We can then choose S and T to simply swap their arguments:
> over,under :: (Bool,Bool) -> V Float (Bool,Bool)
> over (i,j) = return (j,i)
> under (i,j) = return (j,i)
With these choices, the weighting is such that a non-zero weight is assigned to a knot or tangle if and only if all of the labels along a single strand are assigned the same value, in other words we're now summing over ways of assigning labels to entire strands. For rational tangles we can only end up with three possible values corresponding to the three ways the two outputs can be connected to the two inputs. (Straight through, the tangle I called ∞; straight through with a swap, the tangle called -1; and connecting together both the inputs, and both the outputs, the tangle called 0.)
> tangleInfinity,tangleMinus1,tangleZero :: (Bool,Bool) -> V Float (Bool,Bool)
> tangleInfinity (i,j) = return (i,j)
> tangleMinus1 (i,j) = return (j,i)
> tangleZero (i,j) = do
> cup (i,j)
> cap
> test1 = quickCheck $ \x -> (example x == tangleInfinity x)
> test2 = quickCheck $ \x -> (example x == tangleMinus1 x)
> test3 = quickCheck $ \x -> (example x == tangleZero x)
Only test2 succeeds so we know example is a tangle that forms its outputs by swapping the inputs.
So even with this simple assignment we're able to extract some basic connectivity information from our monadic representation. With smarter choices we'll get more information, but that's enough for now. We now have the prerequisites and in the next installment we can start doing some proper knot theory.
> data V r b = V [(r,b)] deriving (Eq,Show)
> unV (V bs) = bs
> instance Num r => Functor (V r) where
> fmap f (V bs) = V $ map (\(r,b) -> (r,f b)) bs
> scale x (bs) = map (\(r,b) -> (x*r,b)) bs
> instance Num r => Monad (V r) where
> return b = V [(1,b)]
> x >>= f = join (fmap f x)
> where join x = g $ fmap unV x
> g (V bs) = V $ concat $ map (uncurry scale) bs
> instance Num r => MonadPlus (V r) where
> mzero = V []
> mplus (V x) (V y) = V (x++y)
> class Num r => VectorSpace r v | v -> r where
> zero :: v
> (.+) :: v -> v -> v
> (.*) :: r -> v -> v
> (.-) :: v -> v -> v
> v1 .- v2 = v1 .+ ((-1).*v2)
> swap (x,y) = (y,x)
> reduce x = V $ filter ((/=0) . fst) $ fmap swap $ M.toList $ M.fromListWith (+) $ fmap swap $ unV $ x
> instance (Num r,Ord b) => VectorSpace r (V r b) where
> zero = V []
> V v1 .+ V v2 = reduce (V (v1 ++ v2))
> r .* V v = reduce (V $ scale r v)