Trace Diagrams with Monads

Knot diagrams aren't the only kind of diagram that can be translated nicely into Haskell monad notation. Other types of diagram include Penrose Spin Networks, many kinds of Feynman Diagram, Penrose Tensor Notation, birdtracks and a type of closely related diagram I hadn't met before: Trace Diagrams.

I encourage readers to check out the Wikipedia page and associated papers on trace diagrams as they give a better tutorial than I could write. My aim here is to show how those diagrams can be translated directly into working code just like with knots.

As usual, this is literate Haskell so I need these lines:

> {-# LANGUAGE MultiParamTypeClasses,FunctionalDependencies,FlexibleInstances #-}

> module Main where

> import qualified Data.Map as M
> import Control.Monad
> infixl 5 .+
> infixl 6 .*

I'll reuse my vector space monad code from before and work in a 3D space with the axes labelled X, Y and Z.

> data Space = X | Y | Z deriving (Eq,Show,Ord)

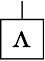
We draw vectors as little boxes with connections emerging from them:


Now recall from my knot posts that we represent a diagram with m legs at the top and n legs at the bottom as an expression that takes an m-tuple as input and returns an n-tuple "in the monad" as output.

Vectors can be represented as elements of V Float Space, for example:

> u,v,w :: V Float Space
> u = return X .- return Y
> v = return X .+ 2.* return Y
> w = return Y .- return Z

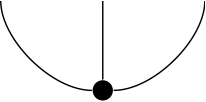
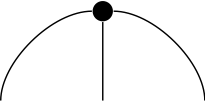
I could have emphasised that there are zero inputs at the top by using type signature () -> V Float Space instead.

Given two vectors we can form their dot product. The dot product itself is represented by a little u-shaped curve:

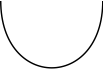
So the dot product of v and w is drawn as:

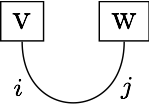
(The i and j are just so you can see what corresponds to what in the code below. They're not really part of the diagram.)

We can implement the dot product as

> cup :: (Space,Space) -> V Float ()
> cup (i,j) = case (i,j) of
>    (X,X) -> return ()
>    (Y,Y) -> return ()
>    (Z,Z) -> return ()
>    otherwise -> 0 .* return ()

and compute an example using

> vdotw = do
>     i <- v
>     j <- w
>     cup (i,j)

We hook up legs of the diagram using corresponding inputs and outputs in the code.

Now consider this diagram:

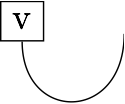
If we attach another vector to the free leg then we get the dot product. So this object is a thing that maps vectors to scalars. Ie. it's a dual vector. So dual vectors are represented by diagrams with a free leg at the top. We can redraw this diagram:
In other words, turning a vector v upside down turns it into a dual vector that takes w to the dot product of v and w. Here's some code for making the dual of v.

> dual :: V Float Space -> Space -> V Float ()
> dual v i = do
>     j <- v
>     cup (i,j)

We can also consider cross products. These take two vectors as input and output one. So we're looking at a diagram with two legs at the top and one at the bottom. We'll use a bold dot to represent one of these:

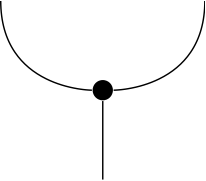
Here's the implementation:

> cross :: (Space,Space) -> V Float Space
> cross (X,Y) = return Z
> cross (Y,Z) = return X
> cross (Z,X) = return Y

> cross (Y,X) = (-1) .* return Z
> cross (Z,Y) = (-1) .* return X
> cross (X,Z) = (-1) .* return Y

> cross _ = mzero

We can form a triple product u.(v×w) like this:

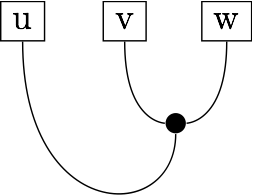
We can then abstract out the triple product bit that looks like this:

Implementing it as:

> trident :: (Space,Space,Space) -> V Float ()
> trident (i,j,k) = do
>    l <- cross (i,j)
>    cup (l,k)

Remember that if u, v and w give the rows of a 3x3 matrix, then u.(v×w) is the determinant of that matrix.

We can also define a dot product for dual vectors that we can draw like this:

The code looks like this:

> cap :: () -> V Float (Space,Space)
> cap () = return (X,X) .+ return (Y,Y) .+ return (Z,Z)

We can now combine the two dot products in a diagram like this:

We can write that as:

> cupcap i = do
>      (j,k) <- cap ()
>      cup (i,j)
>      return k

We'd hope that we could pull this diagram taut and get the identity linear map. If you try applying cupcap to X, Y and Z you'll see it has exactly the same effect as return, which does indeed represent the identity.

(If you allow me to digress, I'll point out that there's something really deep going on with this almost trivial looking identity. It represents the identity map in the sense that it copies the input i to the output k. Imagine we were dealing with the trivial monad, ie. the one that just wraps values. Then no matter how cup and cap were implemented it would be impossible for k to be a copy of i. If you follow the flow of information through that code then i disappears into cup and k is read from cap without it seeing i. If we read from top to bottom we can think of cap as emitting a pair of objects and of cup as absorbing two. There is no way that any information about i can be communicated to k. But in the vector space monad, k can depend on i. As I've mentioned a few times over the years, the universe is described by quantum mechanics which can be described using the vector space monad. Amazingly the above piece of code, or at least something like it, can be physically realised in terms of particles. It describes a process that is fundamentally quantum, and not classical. In fact, Coecke shows that this is a precursor to quantum teleportation in section 3c of this paper. You could also think in terms of information about i being sent back in time through the cap. That's the idea behind this paper on Effective Quantum Time Travel.)

Now we can make a fork by bending down the tines of the cross product:

> fork () = do
>    (i,j) <- cap ()
>    (k,l) <- cap ()
>    m <- cross (j,k)
>    return (i,l,m)

We can write matrices as boxes with a leg for input and a leg for output. Here's an example matrix:

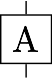
> a :: Space -> V Float Space
> a X = 2 .* return X
> a Y = return Z
> a Z = (-1) .* return Y

It rotates by 90 degrees around the X axis and scales the X axis by a factor of two.

With the help of our two dot products we can turn a matrix upside-down:

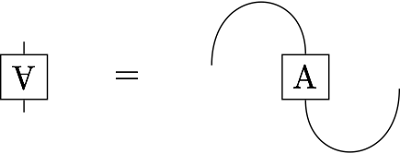
The corresponding code is:

> b :: Space -> V Float Space
> b l = do
>     (i,j) <- cap ()
>     k <- a j
>     cup (k,l)
>     return i

Turning a matrix upside down gives its transpose. You'll find that matrix B rotates in the opposite direction to A but still scales by a factor of two.

Surprisingly, 3! times the determinant of a 3x3 matrix A can be represented by this diagram:

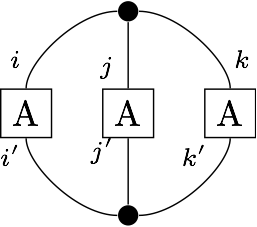
So we can write a determinant routine as follows:

> det a = do
>     (i,j,k) <- fork ()
>     i' <- a i
>     j' <- a j
>     k' <- a k
>     (1/6.0) .* trident (i',j',k')

(Again I've labelled the diagram so you can easily see what corresponds where in the code.)

I could keep going, but at this point I'll just defer to Elisha Peterson's paper. I hope that I've given you enough clues to be able to translate his diagrams into Haskell code, in effect giving semantics for his syntax. As an exercise, try writing code to compute the adjugate of a 3x3 matrix.

And a reminder: none of the above is intended as production-worthy code for working with 3-vectors. It is intended purely as a way to give a practical realisation of trace diagrams allow people to experimentally investigate their properties and make testable conjectures.

And now comes the library code needed to make the above code work:

> swap (x,y) = (y,x)

> class Num k => VectorSpace k v | v -> k where
>    zero :: v
>    (.+) :: v -> v -> v
>    (.*) :: k -> v -> v
>    (.-) :: v -> v -> v
>    v1 .- v2 = v1 .+ ((-1).*v2)

> data V k a = V { unV :: [(k,a)] }
> instance (Num k,Ord a,Show a) => Show (V k a) where
>   show (V x) = show (reduce x)

> reduce x = filter ((/=0) . fst) $ fmap swap $ M.toList $ M.fromListWith (+) $ fmap swap $ x

> instance (Ord a,Num k) => Eq (V k a) where
>  V x==V y = reduce x==reduce y

> instance (Ord a,Num k,Ord k) => Ord (V k a) where
>  compare (V x) (V y) = compare (reduce x) (reduce y)

> instance Num k => Functor (V k) where
>    fmap f (V as) = V $ map (\(k,a) -> (k,f a)) as

> instance Num k => Monad (V k) where
>    return a = V [(1,a)]
>    x >>= f = join (fmap f x)
>        where join x = V $ concat $ fmap (uncurry scale) $ unV $ fmap unV x
>              scale k1 as = map (\(k2,a) -> (k1*k2,a)) as

> instance Num r => MonadPlus (V r) where
>    mzero = V []
>    mplus (V x) (V y) = V (x++y)

> instance (Num k,Ord a) => VectorSpace k (V k a) where
>    zero = V []
>    V x .+ V y = V (x ++ y)
>    (.*) k = (>>= (\a -> V [(k,a)]))

> e = return :: Num k => a -> V k a
> coefficient b (V bs) = maybe 0 id (lookup b (map swap (reduce bs)))

The Three Projections of Doctor Futamura

Introduction

The Three Projections of Futamura are a sequence of applications of a programming technique called 'partial evaluation' or 'specialisation', each one more mind-bending than the previous one. But it shouldn't be programmers who have all the fun. So I'm going to try to explain the three projections in a way that non-programmers can maybe understand too. But whether you're a programmer or not, this kind of self-referential reasoning can hurt your brain. At least it hurts mine. But it's a good pain, right?

So rather than talk about computer programs, I'll talk about machines of the mechanical variety. A bit like computer programs, these machines will have some kind of slot for inputting stuff, and some kind of slot where output will come out. But unlike computer programs, I'll be able to draw pictures of them to show what I'm talking about. I'll also assume these machines have access to an infinite supply of raw materials for manufacturing purposes and I'll also assume that these machines can replicate stuff - because in a computer we can freely make copies of data, until we run out of memory at least.

Minting coins

A really simple example of a machine is one that has a slot for inputting blanks, and outputs newly minted coins:

That's a dedicated $1 manufacturing machine. We could imagine that internally it stamps the appropriate design onto the blank and spits out the result.

It'd be more interesting if we could make a machine with another input slot that allowed us to input the description of the coin. By providing different inputs we could mint a variety of different coins with one machine. I'm going to adopt the convention that when we want to input a description we input a picture of the result we want. I'll draw pictures as rectangles with the subject inside them. Here's a general purpose machine manufacturing pound coins:

The same machine could make dollars, zlotys or yen. You could imagine this machine works by taking the description and then milling the coin CNC style. We call such a machine an interpreter. It interprets the instructions and produces its result.

The interpreter has a great advantage over the dedicated dollar mint. You make make any kind of coin. But it's going to run a lot slower. The dedicated minter can just stamp a coin in one go. The interpreter can't do this because every input might be different. It has to custom mill each coin individually. Is there a way to get the benefits of both types of machine? We could do this: take the coin description and instead of milling the coin directly we mill negative reliefs for both sides of the coin. We then build a new dedicated minting machine that uses these negatives to stamp out the coin. In other words we could make a machine that takes as input a coin description and outputs a dedicated machine to make that type of coin. This kind of machine making machine is called a compiler. It takes a set of instructions, but instead of executing them one by one, it makes a dedicated machine to perform them. Here's one in action:


So here are the two important concepts so far:

Interpreters: these take descriptions or instructions and use them to make the thing described.
Compilers: these take descriptions or instructions and use them to make a machine dedicated to making the thing described. The process of making such a machine from a set of instructions is known as compiling.

The Projections of Doctor Futamura help make clear the relationship between these kinds of things.

Specialisation

We need one more important concept: the specialiser. Suppose we have a machine that has two inputs slots, A and B. But now suppose that when we use the machine we find that we vary the kind of thing we put into slot B, but always end up putting the same thing into slot A. If we know that slot A will always get the same input then we could streamline the machine using our knowledge of the properties of A. This is similar to the minting situation - if we know we're always going to make $1 coins then we can dedicate our machine to that purpose. In fact, if we know that we're always going to input the same thing into slot A we don't even need slot A any more. We could just stick an A inside the machine and whenever the user inputs something to slot B, the machine would then replicate the A and then use it just as if it had been input.

In summary, given a machine with two slots A and B, and given some input suitable for slot A, we could redesign it as a machine with just a B slot that automatically, internally self-feeds the chosen item to A. But we can often do better than this. We don't need to self-feed stuff to slot A. We might be able to redesign the way the machine works based on the assumption that we always get the same stuff going into slot A. For example, in the minting example a dedicate $1 minter was more specialised than just a general purpose minter that interpreted the instructions for making a $1 coin. This process of customising a machine for a particular input to slot A is called specialisation or partial evaluation.

Now imagine we have a machine for automatically specialising designs for machines. It might have two slots: one for inputting a description for a two slot machine with slots A and B, and one for inputting stuff suitable for slot A. It would then print out a description for a customised machine with just a slot B. We could call it a specialisation machine. Here is one at work:

It's converting a description of a two input machine into a description of a one input machine.

The First Projection

The process of specialisation is similar to what I was talking about with dedicated minting machines. Rather than just have a similarity we can completely formalise this. Note that the interpreter above takes two inputs. So the design for an interpreter could be fed into the first input of a specialiser. Now we feed a description the coin we want into slot B. The specialiser whirrs away and eventually outputs a description of a machine that is an interpreter that is dedicated to making that one particular coin. The result will describe a machine with only one input suitable for blanks. In other words, we can use a specialiser as a compiler. This is the first of Doctor Futamura's Projections. Here's a picture of the process at work:

What this shows is that you don't need to make compilers. You can make specialisers instead. This is actually a very practical thing to do in the computing world. For example there are commercial products (I'm not connected with that product in any way) that can specialise code to run on a specific architecture like CUDA. It's entirely practical to convert an interpreter to a compiler with such a tool. By writing a specialiser, the purveyors of such tools allow third parties to develop their own compilers and so this is more useful than just writing a dedicated compiler.

The Second Projection

Time to kick it up a notch. The first input to the specialiser is a description of a two input machine. But the specialiser is itself a two input machine. Are you thinking what I'm thinking yet? We could stuff a description of a specialiser into the specialiser's own first input! In the first projection we provided an interpreter as input to the specialiser. If we know we're always going to want to use the same interpreter then we could streamline the specialiser to work specifically with this input. So we can specialise the specialiser to work with our interpreter like this:

But what is that machine whose description it has output? An interpreter takes as input a description of how to operate on some stuff, like turning blanks into coins. In effect, the output machine has the interpreter built into it. So it takes descriptions and outputs a machine for performing those instructions. In other words it's a compiler. If the specialiser is any good then the compiler will be good too. It won't just hide an interpreter in a box and feed it your description, it will make dedicated parts to ensure your compiler produces a fast dedicated machine. And that is Doctor Futamura's Second Projection.

The Third Projection

But we can go further. The specialiser can accept a description of a specialiser as its first input. That means we can specialise it specifically for this input. And to do that, we use a specialiser. In other words we can feed a descrption of a specialiser into both inputs of the specialiser! Here we go:

But what is the X machine that it outputs? In the second projection we pass in an interpreter as the second argument and get back a compiler. So the third projection gives us a dedicated machine for this task. The X machine accepts the description of an interpreter as input and outputs the description of a compiler. So the X machine is a dedicated interpreter-to-compiler converter. And that is the Third Projection of Doctor Futamura.

If we have a specialiser we never need to make a compiler again. We need only design interpreters that we can automatically convert to compilers. In general it's easier to write interpreters than compilers and so in principle this makes life easier for programmers. It also allows us to compartmentalise the building of compilers. We can separate the interpreter bit from the bit that fashions specific parts for a task. The specialiser does the latter so our would-be compiler writer can concentrate on the former. But who would have guessed that passing a specialiser to itself twice would give us something so useful?

Summary

So here are the projections:

1. Compiling specific programs to dedicated machines.
   
2. Making a dedicated machine for compilation from an interpreter.
   
3. Making a machine dedicated to the task of converting interpreters into compilers.
   

There are lots of variations we can play with. I've just talked about descriptions of things without saying much about what those descriptions look like. In practice there are lots of different 'languages' we can use to express our descriptions. So variations on these projections can generate descriptions in different languages, possibly converting between them. We might also have lots of different specialisers that are themselves optimised for specific types of specialisation. The Futamura projections give interesting ways to combine these. And there are also variations for generating dedicating machines for other tasks related to compiling - like parsing the descriptions we might feed in as input. If you want to read more on this subject there's a whole book online with example code. They're not easy things to design. I think that specialisation is a killer feature that I'd like to see more of. Present day compilers (and here I'm talking about computers, not machines in general) are hard-coded black boxes for the task of compilation. They're not very good at allowing you to get in there and tweak the way compilation occurs - for example if you want to generate code according to a strategy you know. Specialisation is a nice alternative to simply bolting an API onto a compiler. It would make it easy for anyone to write optimising and optimised compilers for their own languages and combine such compilers with interpreters for interactive instead of offline compilation. I learnt about this stuff, as well as lots of other stuff in my blog, from the excellent Vicious Circles. The theory is closely related to the theory of writing quines that I used for my three language quine. And if you keep your ears to the ground you can hear rumours of a fabled fourth projection...

---

Appendix

I wanted to address some of the comments so I've added an appendix where I use the Haskell type checker to tighten up the statements I make above. There are some places I made some choices and I decided to make the specialiser output machines rather than pictures. This code doesn't actually do anything.

One important thing to note is that with these definitions the first projection is a function describing the action of a machine after it has been given one input. The second and third projections are dedicated machines.

> module Futamura where

I'm using P a to represent the type of a Picture (or Plan, or Program) of how to perform an operation of type a and M a to represent a Machine (or executable) that executes such an operation.

I use M because I want to make explicit what is actually a machine. In Haskell a type a -> b -> c can be thought of as a machine that takes an input of type a and an input of type b and outputs a c, or as a machine that takes as input an a and outputs another machine that makes a c from a b. I distinguish those by using M (a -> b -> c) for the former and M (a -> M (b -> c)) for the latter.

I'm not actually going to built a Futamura specialiser so the right hand sides hare are just filler:

> data P a = P
> data M a = M

Running a machine gives a way to perform what the machine is designed to do. We're not really running machines in Haskell so we have an undefined right hand side.

> run :: M a -> a
> run = undefined

A specialiser is a machine that takes as first input a picture of a process mapping an a and a b to a c. It also takes as argument the specialised value for the input for the process. It then outputs a dedicated machine for the specialised process:

> specialise :: M (P (a -> b -> c) -> a -> M (b -> c))
> specialise = undefined

We actually need the picture of the specialiser as it's going to be specialised:

> specialisePicture :: P (P (a -> b -> c) -> a -> M (b -> c))
> specialisePicture = undefined

For the first projection we'll need an interpreter. An interpreter is a general purpose machine that takes pictures of how to map an a to a b, as well as an actual a, and can then give you a b:

> interpreter :: M (P (a -> b) -> a -> b)
> interpreter = undefined

And what we really need is a picture of an interpreter:

> interpreterPicture :: P (P (a -> b) -> a -> b)
> interpreterPicture = undefined

The first projection turns a picture into a dedicated machine. So it functions as a compiler. But note that it's not itself a dedicated machine. It's a general purpose machine which acts as a compiler when given (a picture of) an interpreter as first input:

> proj1 :: P (input -> output) -> M (input -> output)
> proj1 = run specialise interpreterPicture

The second projection is a dedicated machine that does the task of proj1. So it's a compiler:

> proj2 :: M (P (input -> output) -> M (input -> output))
> proj2 = run specialise specialisePicture interpreterPicture

An interpreter is something that can take a computer program and some input and generate the output you expect from the program. A compiler, on the other hand, converts programs into dedicated machines to process the input into the output. And that's exactly what the third projection does:

> proj3 :: M (P (program -> input -> output) -> M (program -> M (input -> output)))
> proj3 = run specialise specialisePicture specialisePicture

---