A pictorial proof of the hairy ball theorem
The hairy-ball theorem says that there is no continuous non-zero vector field on the surface of a sphere. There are lots of popular accounts that tell you what this means, giving great examples. Here's a Youtube video for example:
My goal is to show why it's always true.
A simply connected domain in the plane is one with the property that any loop in it can be shrunk down to a point. Here's an example of a domain D with an example loop L being shrunk down to a point P:
Here's an example of a domain that's not simply connected. It has a hole in the middle. I've drawn a L loop around the hole. You can't shrink that loop to a point because the hole gets in the way:
Here's a simply connected domain with a vector field on it:
Think of the vectors as being drawn literally in the surface so that if we were to pick up the surface and stretch it like a piece of rubber the vectors would get stretched with it. Remember that a vector field is defined everywhere in the domain so the arrows are just a random sprinkling of examples to show what's going on. For this to be an accurate picture you want to imagine an infinity of arrows, one at every single point of the domain.
Let's put a loop, starting and ending at P, in our simply-connected domain:
Now imagine travelling along the loop, starting at P and ending at P. As you move along there's an arrow at each point in your journey. Here's what the arrows look like as you travel from P to P anti-clockwise, plotted as a kind of graph:
The vectors start off pointing to the right. They swing anti-clockwise by about 45º and then swing back to where they started. As the journey is a loop they clearly must end where they started. A different, really swirly vector field, might have resulted in arrows that that rotated around hundreds of times along your journey. But by time you reach the end of the journey they must swing back to where they started. What's slightly less obvious is that they'd also have to rotate back to cancel out the hundreds of swings. You might think "the vectors could rotate round a hundred times but as long as they make exactly 100 turns they'll return to where they started and there's no need for them to unwind". But actually, every bit of rotation in the journey must be unwound. The total amount of rotation, adding all the positive rotations, and subtracting off the negative rotations, is called the winding number for the loop. We count anti-clockwise rotation as positive and clockwise as negative. So I'm claiming that the winding number for a closed loop in a simply-connected domain is always zero.
(Note: in most books the winding number normally refers to how many times the loop itself winds around a point. I'm using it to refer to how many times the vector winds around itself you follow the loop. To help with your intuition: the hour hand of a working clock normally accumulates a winding number of -2 in one day. If it ran forward for a day, but then ran backwards for half a day, the winding number would be -1.)
Here's why the winding number for simply connected domains must be zero: firstly - it's pretty clear that the winding number for any loop must be an integer. If the winding number was a half, say, the arrow wouldn't end up pointing 180º from where it started which makes no sense for a closed loop. Now the domain is simply connected, so the loop can be shrunk to a point. Now imagine doing the shrinking really slowly and keeping track of the winding number as the loop shrinks. As the loop shrinks, the graph of the vectors along the loop must vary slowly. The total winding number depends continuously on the vectors in the graph so the winding number must vary slowly as the loop shrinks. But the winding number is an integer. It can't change really slowly, it can only change by amounts of a whole integer. So the winding number can't change at all. Every loop in a simply-connected domain must have a winding number that's the same as the winding number of a loop that is just one point ie. zero.
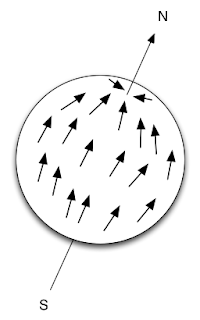
On to the sphere. Here's a sphere with a vector field where all of the vectors point along lines of longitude to the north pole:
(Sorry about my poor quality drawing but I'm sure you know what vectors pointing north look like.)
At this point you may be tempted to say "aha! That's a continuous vector field on the sphere that's non-zero everywhere!" Alas, it's not defined everywhere. It's a vector field everywhere except at the north and south poles. If you're at the north pole, no non-zero vector can point north. And at the south pole every non-zero vector points north with no continuous way to pick just one.
Given any vector field on the Earth we can imagine slicing the earth through the equator and flattening out the surfaces of the northern and souther hemispheres as two separate disks. Here's what you get if you do this with the north vector field (ignoring the problems at the poles for now):
Suppose we start at the point P and follow a loop eastwards along the equator. That's an anti-clockwise loop round the upper disk and simultaneously a clockwise loop round the lower disk. Here are the graphs:
But here's the most important thing in this proof: the winding number for the upper hemisphere loop will be two more that the winding number for the lower hemisphere loop, no matter what vector field you have. This is because if you've travelled an angle θ around the equator, the vectors at opposite ends of the orange arrows will differ by an angle of 2θ. For example, once you're 90º around the earth, the north arrow is draw as a down-arrow in the upper graph and as an up-arrow in the lower graph. They're already 180º apart. You can see this is true for north pointing vectors literally by tracing with your fingers around the loops. It's also true for vectors pointing east. I'll leave that as an exercise for you, but here's a picture of some eastward vectors to get you started:
Along the equator, every vector on the surface is a linear combination of north and east vectors. So if it's true for both the north and east vectors then it must be true for all vectors. But if the graph for one picture of the equatorial loop has vectors that are 2θ more than the vectors for another graph, the first one must complete two revolutions more than the second one. So the first has a winding number two more than the second.
If you had a continuous vector field that really was non-zero over the entire sphere, cutting the sphere in half would give a pair of continuous vector fields defined on disks. As disks are simply-connected, the theorem we started with tells us they must both have winding number zero as you loop around them. But we've also just shown that looping round one has winding number two more than looping around the other. This is a contradiction. So there is no continuous vector field that is non-zero everywhere. ∎
If you get stuck above I strongly recommend trying to draw some continuous non-zero vector fields on the sphere, transferring them to disks, and counting winding numbers.
Notice how we've done more than prove the theorem. We now know that if we have a continuous vector field on a sphere we can find out whether to look for its zeros in the northern or southern hemisphere by computing the winding numbers as above. At least one of the two winding numbers must be non-zero and that tells us which hemisphere we can be sure contains a zero. The fact that the two winding numbers differ by two, and not by just one, also tells us a bit about the nature of the zeros. But that's another story. That two is also related to the fact that the Euler characteristic of the sphere is two. It's also related to the Lefschetz index
This proof is based on proofs I studied years ago relating to Chern classes. I recently became interested in Chern classes again because they play an important role in understanding phenomena in solid state physics such as the quantum Hall effect. That argument about slowly shrinking a loop leaving its winding number unchanged tells you a lot about slowly changing certain types of quantum system.
It's possible I completely messed up. Here's an "elementary" proof. It looks much harder than what I did. But I feel like I did faithfully capture, in pictures, an argument that's buried in Lectures on Riemann surfaces. And it seems to correctly reproduce the Lefschetz number of 2.