Categories of polynomials and comonadic plumbing
Suppose you have a Haskell program and you want to introduce a new global constant into your program. There are at least two approaches you could take:
Now I’m going to roughly sketch a more categorical view of both of these approaches. So let’s restrict ourselves to the subset of Haskell that corresponds to typed lambda calculus without general recursion so that we know all of our functions will be total and correspond to the mathematical notion of a function. Then all of our functions become arrows in the category that we’ll call Hask.
Firstly consider approach (1). Suppose we want to introduce a new constant, x, of type A. Category theory talks about arrows rather than elements of objects, so instead of introducing x of type A, introduce the function x:1->A where 1 is the terminal object in Hask, normally called (). An element of A is the same thing as an element of 1->A, but in the latter case we have an arrow in the category Hask.
Before continuing, let me digress to talk about polynomials. Suppose we have a ring (with an identity) R. We define R[x], where x is an indeterminate, to be the ring of polynomials in x. Another way to describe that is to say that R[x] is the smallest ring containing R and an indeterminate x, that makes no assumptions about x other than those required to make R[x] a ring. For example we know that (1+x)(1-x)=1-x2, because that must hold in any ring. Given a polynomial p in R[x] we can think of it as a function fp from R to R. fp(a) is the value we get when substituting the value of a for x in p. So a polynomial in R[x] is the same as a function from R to R that can be written in terms of elements of R, multiplication and addition.
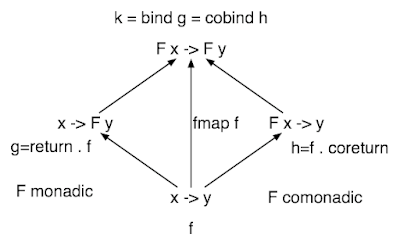
We can do the same with category theory. Given a category A we can ask for the smallest category extending A and containing an indeterminate arrow x:1 -> A. Just as with polynomials we have to allow all possible arrows that can be made by composing arrows of A with x. The resulting expressions for arrows will contain x as a free variable, just like the way x appears in polynomials. In fact, by analogy we can call the resulting category, A[x], the category of polynomials in x:1->A. In the special case A=Hask, you can see that Hask[x] is the category of Haskell functions extended by a new constant of type x:1->A but assuming no equations other than those necessary to make Hask[x] a category. Just as an arrow in Hask is a Haskell function, an arrow in Hask[x] is a Haskell function making use of an as yet undefined constant x.
(I've glossed over some subtleties. Just as we need a suitable equivalence relation to ensure that (1+x)(1-x)=1-x2 in R[x], we need suitable equivalence relations in our category. I'll be showing you where to find the missing details later.)
Here's the implementation of a function, h, making use of a constant x:
(Note that I'll be using Edward Kmett's category-extras shortly so I need some imports)
Now consider the second approach. The easiest thing is to just give an implementation of the above using the reader monad:
Note how, as is typical in monadic code, I have to plumb f' and g' together using >>= so that 1.23456 is passed through f' and g'. Previously I've described another way to think about the composition of monadic functions. Using >>= we can compose functions of type a->m b and b->m c to make a function of type a->m c. The result is that given a monad we can form the Kleisli category of the monad. The objects are the same as in Hask, but an arrow from a->b in the Kleisli category is an arrow of type a->m b in Hask. It's not hard to show this satisfies all of the axioms of a category. When we program in the reader monad it's a bit like we've stopped using Hask and switched to the Kleisli category of the reader monad. It's not quite like that because we used functions like +. But in theory we could use lifted versions of those functions too, and then we'd be programming by composing things in the Kleisli category. If we call the reader monad R then we can call the corresponding Kleisli category HaskR. (Strictly speaking that R needs a subscript telling is the type of the value we intend to ask for.)
So here's the important point: Hask[x] is the same category as HaskR. In both cases the arrows are things, which when supplied a value of the right type (like 1.23456), give arrows in Hask from their head object to their tail object.
But there's another way to do this. We can use the reader comonad:
In a similar way, we're dealing with arrows of the form wa -> b and we can compose them using =>>. These arrows form the coKleisli category of the reader comonad, S, which we can write HaskS. So we must have
Now some back story. Over 20 years ago I was intrigued by the idea that logic might form a category with logical ‘and’ and ‘or’ forming a product and coproduct. I came across the book Introduction to Higher Order Categorical Logic by Lambek and Scott for ₤30.00. That’s ₤60.00 at today's prices, or about $120.00. On a student grant? What was I thinking? And as it bore no relation to anything I was studying at the time, I barely understood a word of it. I was probably fairly applied at that point doing courses in stuff like solid state physics and electromagnetism as well as a bit of topology and algebra. I doubt I'd heard of lambda calculus though I could program in BASIC and APL. So there it sat on my bookshelf for 22 years. Periodically I’d look at it, realise that I still didn’t understand enough of the prerequisites, and put it back on the shelf. And then a month or so ago I picked it up again and realised that the first third or so of it could be interpreted as being about almost trivial Haskell programs. For example, on page 62 was
The language is a little different. Lambek and Scott used the term cotriple instead of comonad and Kleisli category where I’d say coKleisli category. δ and ε are cojoin and coreturn. And Lambek and Scott's theorem applies to any cartesian closed category. But after staring at this claim for a while it dawned on me that all it was really saying was this: here are two ways to introduce new constants into a category. But there’s no way I would have seen that without having practical experience of programming with monads. Learning Haskell has finally paid off. It’s given me enough intuition about category theory for me to get some return on my ₤30.00 investment paid to Heffers all those years ago. I expected to take this book to my deathbed, never having read it.
Anyway, for the details I left out above, especially the correct equivalence relation on Hask[x], you'll just have to read the book yourself.
Also, note the similarity to the deduction theorem. This theorem says that if we can prove B, assuming A, then we can deduce A implies B without making any assumptions. It unifies two way to introduce a proposition A, either as a hypothesis, or as an antecedent in an implication. In fact, the above theorem is just a categorical version of the deduction theorem.
Also note the connection with writing pointfree code. In fact, the pointfree lambdabot plugin makes use good use of the reader monad to eliminate named parameters from functions.
I’m amazed by seeing a book from 1986 that describes how to use a comonad to plumb a value through some code. As far as I know, this predates the explicit use of the reader monad in a program, Wadler and Moggi’s papers on monads, and certainly Haskell. Of course monads and comonads existed in category theory well before this date, but not, as far as I know, for plumbing computer programs. I’d love to hear from anyone who knows more about the history these ideas.
- Simply introduce a new global constant. You could name it x and write something like x=1.23456 and refer to x throughout your code. This has the advantage of being easy to implement.
- Write all of your code in monadic style and make use of the reader monad. This is intrusive in the sense that you may have to make many changes to your code to support it. But it has the advantage that all of your functions now explicitly become functions of your global constant.
Now I’m going to roughly sketch a more categorical view of both of these approaches. So let’s restrict ourselves to the subset of Haskell that corresponds to typed lambda calculus without general recursion so that we know all of our functions will be total and correspond to the mathematical notion of a function. Then all of our functions become arrows in the category that we’ll call Hask.
Firstly consider approach (1). Suppose we want to introduce a new constant, x, of type A. Category theory talks about arrows rather than elements of objects, so instead of introducing x of type A, introduce the function x:1->A where 1 is the terminal object in Hask, normally called (). An element of A is the same thing as an element of 1->A, but in the latter case we have an arrow in the category Hask.
Before continuing, let me digress to talk about polynomials. Suppose we have a ring (with an identity) R. We define R[x], where x is an indeterminate, to be the ring of polynomials in x. Another way to describe that is to say that R[x] is the smallest ring containing R and an indeterminate x, that makes no assumptions about x other than those required to make R[x] a ring. For example we know that (1+x)(1-x)=1-x2, because that must hold in any ring. Given a polynomial p in R[x] we can think of it as a function fp from R to R. fp(a) is the value we get when substituting the value of a for x in p. So a polynomial in R[x] is the same as a function from R to R that can be written in terms of elements of R, multiplication and addition.
We can do the same with category theory. Given a category A we can ask for the smallest category extending A and containing an indeterminate arrow x:1 -> A. Just as with polynomials we have to allow all possible arrows that can be made by composing arrows of A with x. The resulting expressions for arrows will contain x as a free variable, just like the way x appears in polynomials. In fact, by analogy we can call the resulting category, A[x], the category of polynomials in x:1->A. In the special case A=Hask, you can see that Hask[x] is the category of Haskell functions extended by a new constant of type x:1->A but assuming no equations other than those necessary to make Hask[x] a category. Just as an arrow in Hask is a Haskell function, an arrow in Hask[x] is a Haskell function making use of an as yet undefined constant x.
(I've glossed over some subtleties. Just as we need a suitable equivalence relation to ensure that (1+x)(1-x)=1-x2 in R[x], we need suitable equivalence relations in our category. I'll be showing you where to find the missing details later.)
Here's the implementation of a function, h, making use of a constant x:
(Note that I'll be using Edward Kmett's category-extras shortly so I need some imports)
> import Control.Monad.Reader
> import Control.Comonad
> import Control.Comonad.Reader
> x = 1.23456
> f a = 2*a+x
> g a = x*a
> h a = f (g a)
> test1 = h 2
Now consider the second approach. The easiest thing is to just give an implementation of the above using the reader monad:
> f' a = do
> x <- ask
> return $ 2*a+x
> g' a = do
> x <- ask
> return $ x*a
> h' a = return a >>= g' >>= f'
> test2 = runReader (h' 2) 1.23456
Note how, as is typical in monadic code, I have to plumb f' and g' together using >>= so that 1.23456 is passed through f' and g'. Previously I've described another way to think about the composition of monadic functions. Using >>= we can compose functions of type a->m b and b->m c to make a function of type a->m c. The result is that given a monad we can form the Kleisli category of the monad. The objects are the same as in Hask, but an arrow from a->b in the Kleisli category is an arrow of type a->m b in Hask. It's not hard to show this satisfies all of the axioms of a category. When we program in the reader monad it's a bit like we've stopped using Hask and switched to the Kleisli category of the reader monad. It's not quite like that because we used functions like +. But in theory we could use lifted versions of those functions too, and then we'd be programming by composing things in the Kleisli category. If we call the reader monad R then we can call the corresponding Kleisli category HaskR. (Strictly speaking that R needs a subscript telling is the type of the value we intend to ask for.)
So here's the important point: Hask[x] is the same category as HaskR. In both cases the arrows are things, which when supplied a value of the right type (like 1.23456), give arrows in Hask from their head object to their tail object.
But there's another way to do this. We can use the reader comonad:
> f'' a = 2*extract a+askC a
> g'' a = extract a*askC a
> h'' a = a =>> g'' =>> f''
> test3 = runCoreader (h'' (Coreader 1.23456 2))
In a similar way, we're dealing with arrows of the form wa -> b and we can compose them using =>>. These arrows form the coKleisli category of the reader comonad, S, which we can write HaskS. So we must have
Hask[x]≅HaskR≅HaskS.
Now some back story. Over 20 years ago I was intrigued by the idea that logic might form a category with logical ‘and’ and ‘or’ forming a product and coproduct. I came across the book Introduction to Higher Order Categorical Logic by Lambek and Scott for ₤30.00. That’s ₤60.00 at today's prices, or about $120.00. On a student grant? What was I thinking? And as it bore no relation to anything I was studying at the time, I barely understood a word of it. I was probably fairly applied at that point doing courses in stuff like solid state physics and electromagnetism as well as a bit of topology and algebra. I doubt I'd heard of lambda calculus though I could program in BASIC and APL. So there it sat on my bookshelf for 22 years. Periodically I’d look at it, realise that I still didn’t understand enough of the prerequisites, and put it back on the shelf. And then a month or so ago I picked it up again and realised that the first third or so of it could be interpreted as being about almost trivial Haskell programs. For example, on page 62 was
Proposition 7.1
The category A[x] of all polynomials in the indeterminate x:1->A over the cartesian or cartesian closed category A is isomorphic to the Kleisli category AA=ASA of the cotriple (SA,&epsilonA,δA).
The language is a little different. Lambek and Scott used the term cotriple instead of comonad and Kleisli category where I’d say coKleisli category. δ and ε are cojoin and coreturn. And Lambek and Scott's theorem applies to any cartesian closed category. But after staring at this claim for a while it dawned on me that all it was really saying was this: here are two ways to introduce new constants into a category. But there’s no way I would have seen that without having practical experience of programming with monads. Learning Haskell has finally paid off. It’s given me enough intuition about category theory for me to get some return on my ₤30.00 investment paid to Heffers all those years ago. I expected to take this book to my deathbed, never having read it.
Anyway, for the details I left out above, especially the correct equivalence relation on Hask[x], you'll just have to read the book yourself.
Also, note the similarity to the deduction theorem. This theorem says that if we can prove B, assuming A, then we can deduce A implies B without making any assumptions. It unifies two way to introduce a proposition A, either as a hypothesis, or as an antecedent in an implication. In fact, the above theorem is just a categorical version of the deduction theorem.
Also note the connection with writing pointfree code. In fact, the pointfree lambdabot plugin makes use good use of the reader monad to eliminate named parameters from functions.
I’m amazed by seeing a book from 1986 that describes how to use a comonad to plumb a value through some code. As far as I know, this predates the explicit use of the reader monad in a program, Wadler and Moggi’s papers on monads, and certainly Haskell. Of course monads and comonads existed in category theory well before this date, but not, as far as I know, for plumbing computer programs. I’d love to hear from anyone who knows more about the history these ideas.
Labels: comonads, haskell, mathematics, monad